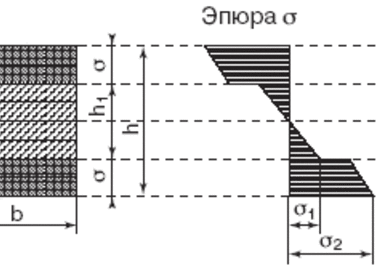
Размеры досок, выпиливаемых параллельно продольной оси бревен

Известно, что практическое решение задач составления рациональных поставов затруднено тем, что для досок, входящих в постав, должны существовать оптимальные по толщине, ширине и длине размеры, зависящие от величины диаметра и коэффициента сбега бревна, способа его распиловки, количества досок в поставе, толщины применяемого режущего инструмента, необходимости выпиливать сечения пиломатериалов по спецификации потребителя.
Характер изменения оптимальных ширин обрезных досок, выпиливаемых параллельно продольной оси из боковой зоны бревен, форма которых приравнена к усеченному параболоиду или усеченному конусу, в зависимости от коэффициентов сбега бревен и положения досок в поставе представлен на рис. 1.
С увеличением коэффициента сбега значение оптимальной ширины досок для бревен исследуемых форм увеличивается. С увеличением величины охвата пластей досок поставом (т. е. с увеличением расстояния от центра бревна до наружных пластей досок) значения оптимальных ширин уменьшаются.
Относительная разность (в %) величин оптимальных ширин досок для бревен сравниваемых форм представлена на графике (рис. 2).

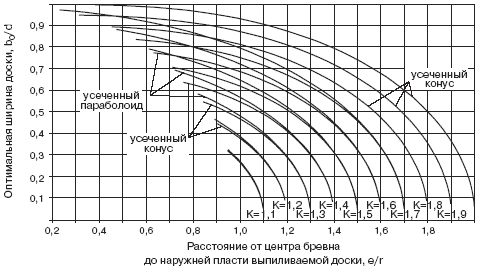
Рис. 1. Изменение величин оптимальных ширин досок, выпиливаемых из боковой зоны бревен параболической и конической формы

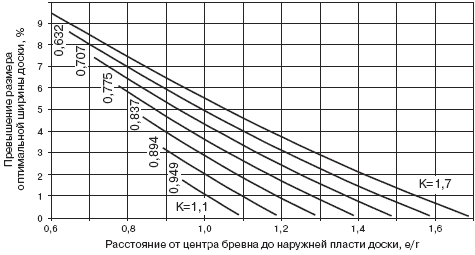
Рис. 2. Превышение размеров оптимальных ширин обрезных досок, выпиленных из боковой зоны бревен различной формы

При Ei >= Eпиф.к наибольшее превышение размеров оптимальных ширин досок, выпиливаемых из бревен с формой ствола усеченный параболоид, в сравнении с бревнами формой усеченный конус, составляет: 9,95% для бревен, имеющих коэффициент сбега К = 1,7; 8,71% при К = 1,6; 7,42% при К = 1,5; 6,07% при К = 1,4; 4,65% при К = 1,3; 3,17% при К = 1,2; 1,63% при К = 1,1.
С увеличением охвата относительная разность уменьшается.
Максимальное расстояние Eпиф.к между симметричными наружными пластями необрезных досок, при котором их обрезают, начиная с вершинного диаметра по всей длине бревна, формой ствола которого является усеченный конус, вычисляют из условия [1]:

, (1)

откуда . (2)

Из выражения (2) видно, что величина Eпиф.к зависит от величины коэффициента сбега бревна и при К = 2,0 принимает нулевое значение.
При Ei ? Eпиф.к оптимальная длина выпиливаемой доски равна длине бревна, т. е. l0 = L, а оптимальную ширину доски рассчитывают по его вершинному диаметру:

.
При Ei > Eпиф.к оптимальную длину и оптимальную ширину досок определяют по формулам:

, (3)

. (4)

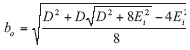
Характер изменения величины Епиф. в зависимости от коэффициентов сбега и формы бревен показан на рис. 3. Из графика (рис. 3) видно, что с увеличением коэффициента сбега бревна значения Епиф. уменьшаются независимо от вида формы бревен, а разница этих значений увеличивается. При изменении коэффициента сбега от К = 1,1 до К = 1,4 величина Епиф. изменяется: для бревен, имеющих форму усеченного параболоида от 0,946d до 0,721d, для усеченного конуса — соответственно от 0,948d до 0,775d.

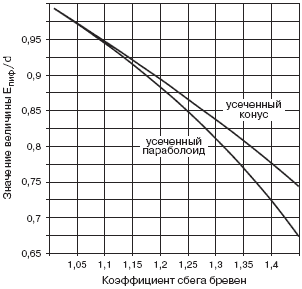
Рис. 3. Изменение величины Епиф.

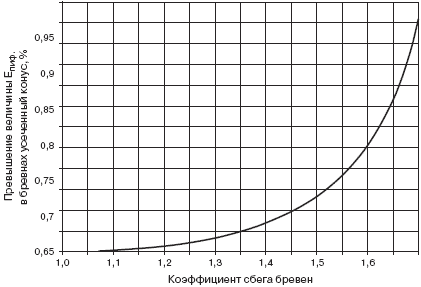
Рис. 4. Превышение величины Епиф. в бревнах, имеющих форму усеченного конуса

Значение величины Епиф. у бревен, имеющих форму усеченного параболоида, меньше, чем у бревен с формой усеченного конуса при соответствующих коэффициентах сбега. Это можно объяснить тем, что объем зоны сбега усеченного параболоида больше объема сбега усеченного конуса.
Отмеченное выше указывает также на то, что выход обрезных длинномерных пиломатериалов (т. е. без укорочения) из бревен с меньшим коэффициентом сбега всегда будет выше, чем из бревен с большим коэффициентом сбега. При одинаковом диаметре и коэффициенте сбега бревна объемный выход (в %) длинномерных обрезных пиломатериалов из бревен, с формой ствола, приравненной к усеченному конусу, будет больше, чем из бревен с формой ствола в виде усеченного параболоида.
Характер превышения Р%, в %, величины Епиф. в бревнах, имеющих форму усеченного конуса, в сравнении с имеющими вид усеченного параболоида, при различных коэффициентах сбега представлен на графике (рис. 4).
Приведенный график построен по отношению разности величин Епиф. в бревнах различной формы к величине Епиф.к:

, (5)

где Епиф.к и Епиф.п. — величины пифагорической зоны в бревнах, имеющих соответственно форму усеченного конуса и усеченного параболоида (т. е. зоны, в которой доски оптимальной ширины не укорачивают).
Из графика (рис. 4) видно, что при коэффициентах сбега К = 1,1; К = 1,2; К = 1,3; К = 1,4; К = 1,5; К = 1,6; К = 1,7 величина Р% принимает соответственно значения 0,28; 1,26; 3,27; 6,91; 13,4; 25,84; 57,18%.
Характер изменения оптимальных длин обрезных досок, выпиливаемых из боковой зоны бревен различной формы в зависимости от величин охвата и коэффициентов сбега, показан на графике (рис. 5). На этом графике кривые для усеченного параболоида построены по уравнению:

, (6)

а для усеченного конуса — по уравнению (3).
При охвате Еi > d оптимальная длина обрезных досок, выпиливаемых из боковых зон бревен формы усеченный конус, меньше, чем из бревен, имеющих вид усеченного параболоида.
Величину относительной разности размеров оптимальных длин пиломатериалов, выпиливаемых из боковых зон бревен различной формы, можно определить по графику (рис. 6).
При Ei = d необрезная доска ограничена полной гиперболой или параболой, при этом ее длина будет равна длине бревна.

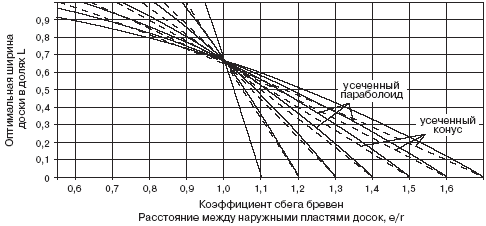
Рис. 5. Изменение оптимальной длины обрезных досок, выпиливаемых из бревен различной формы

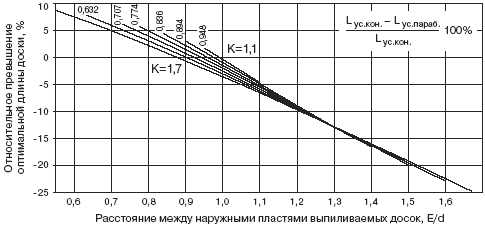
Рис. 6. Относительная разность величин оптимальных длин обрезных досок, выпиливаемых из боковой зоны бревен различной формы

Из графиков (рис. 6) видно, что в сравниваемых случаях длина обрезных досок, выпиленных из бревен, имеющих форму усеченного параболоида, при К = 1,1; К = 1,2; К =1,3; К = 1,4; К = 1,5; К = 1,6 и К = 1,7 будет превышать сравниваемую соответственно на 0,55; 1,1; 1,63; 2,16; 2,68; 3,2 и 3,7%.
При Ei ? Епиф. объем обрезных досок, выпиленных из бревен любой формы, вычисляют по уравнению:

. (7)
При Ei > Епиф.к объем обрезных досок оптимальных размеров, выпиленных из бревна, форма которого приравнена к усеченному конусу, вычисляют по уравнению:

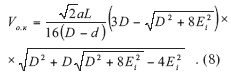
При Ei > Епиф.п объем обрезных досок оптимальных размеров, выпиленных из бревна, форма которого приравнена к усеченному параболоиду, вычисляют по уравнению:

. (9)

На графике (рис. 7) дан характер изменения объемов обрезных досок оптимальных размеров, выпиливаемых из боковой зоны бревен различной формы. Анализируя вышеприведенные графики (рис. 7), отметим, что при Еi > Eпиф. объем досок оптимальных размеров, выпиливаемых из боковой зоны бревен, имеющих форму усеченного параболоида, больше, чем из бревен с формой усеченного конуса. Величина такого превышения показана на графиках (рис. 8). При Ei > Епиф.к с увеличением охвата относительная разность величин объемов досок оптимальных размеров увеличивается.
При одинаковой величине охвата наружных пластей выпиливаемых досок с увеличением коэффициента сбега бревен разность объемов выпиливаемых досок увеличивается. Так, например, для Ei = d при коэффициентах сбега бревен К = 1,1; К = 1,2; К = 1,3; К = 1,4 и К = 1,5 такая разность составляет соответственно 1,62; 3,09; 4,44; 5,68 и 6,84%. При Ei = 1,05d такая разность будет составлять соответственно 3,11; 4,44; 5,66; 6,80 и 7,86%.
При Ei = Епиф. относительная разность величин объемов обрезных досок оптимальных размеров для всех коэффициентов сбега бревен не превышает 1%.

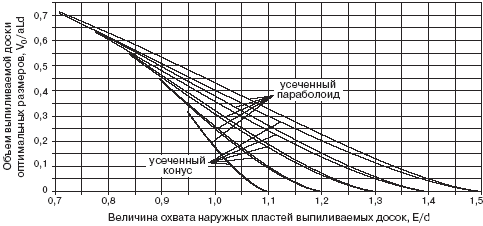
Рис. 7. Характер изменения объемов обрезных досок оптимальных размеров, выпиливаемых из бревен различной формы

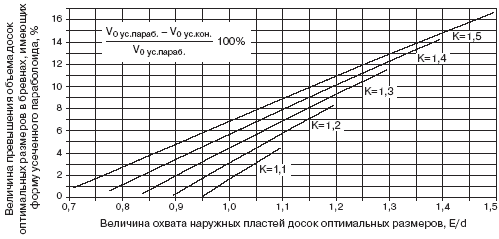
Рис. 8. Относительная разность величин объемов досок оптимальных размеров, выпиливаемых из боковой зоны бревен различной формы

Литература
1. Уласовец В.Г. Рациональный раскрой пиловочника: моногр. /В.Г. Уласовец. — Екатеринбург: Урал. гос. лесотехн. ун-т, 2003. — 278 с.

---