Соотношение несущей способности и главной предельно допустимой нагрузки для отожженного стекла
Предпосылки
Архитектурное остекление в зданиях обычно состоит из простых тонких прямоугольных
листов стекла, закрепленных на несущей конструкции. Вследствие большого
соотношения габаритов стекла к его толщине, стеклянная панель рассчитывается
как большая тонкая пластина. Большая величина прогиба или деформации по
сравнению с толщиной панели приводит помимо изгиба к существенным напряжениям
в панели подобно нагрузке на мембрану. Толщина панели, прямоугольная поверхность,
соотношение сторон и максимальное значение поперечной нагрузки приводят
к разному взаимному сочетанию поведения панели как мембраны и сопротивлению
стекла напряжению изгиба.
Отожженное стекло — хрупкий материал, могущий разрушаться при нагрузках
существенно ниже, чем рассчитывается в материаловедении, из-за влияния
на прочность стекла дополнительных неучтенных факторов. Гриффит (Griffith)
[2] объясняет это явление наличием на поверхности стекла микроцарапин,
микротрещин и других микроскопических пороков на поверхности материала,
которые могут естественным образом формироваться при охлаждении материала
и неполной кристаллизации. Пары воды, замерзая, в сочетании с другими
нагрузками растяжения могут изменять форму поверхностных трещин и приводить
к накоплению в них существенных напряжений. Такие концентраторы напряжений
со временем существенно снижают несущую способность стекла [3]. Продолжительность
приложения нагрузки также становится фактором, влияющим на прочность стекла.
Предыдущие попытки моделирования сопротивления нагрузке (LR) оконного
стекла опирались на эмпирические наблюдения и зависимости для учета влияния
микропороков на поверхности стекла на его несущую способность, и точность
такого прогнозирования была проблематичной. Разные исследователи [4],
[5], [6] разработали эмпирические модели определения LR оконного стекла,
используя разные сочетания размеров прямоугольной оконной панели, ее толщины
и продолжительности воздействия нагрузки. В этих экспериментах всякий
раз использовались новые, еще неразрушенные образцы стеклянных панелей.
Данные этих ранее проведенных экспериментов легли в основу различных строительных
регламентов и вошли в методики по проектированию [7], [8], [9]. Эти методики
проектирования обеспечили появление простого способа определения LR для
монолитного отожженного стекла как функцию площади поверхности стекла
и его толщины, используя прямолинейный график. Эти строительные нормы
и правила не ссылались прямо на эффект влияния поверхностных микротрещин
на прочность. Вдобавок, эти графики в строительных нормах не учитывали
соотношения сторон прямоугольника в качестве фактора влияния на величину
LR оконного стекла.
Некоторые другие исследователи создали численные модели для прогнозирования
величины LR оконного стекла. Цай и Стюарт (Tsai, Stewart [10]) использовали
численный метод конечных элементов для расчета нагрузок в оконном стекле
при равномерно распределенной поперечной нагрузке. Исследователи установили,
что их метод не вполне применим именно к определению расчетной LR оконного
стекла, но что он довольно точно рассчитывает нагрузки и деформации при
равномерно распределенной поперечной нагрузке до уровня 20,6 МПа. Эта
модель хорошо согласовалась с данными экспериментов и учитывала фактор
влияния соотношения сторон, но не была адекватной для определения расчетной
LR оконного стекла, поскольку не учитывала влияние микротрещин и продолжительность
нагрузки.
Американская корпорация PPG опубликовала ряд конструкций и графики к ним
на основе модели Цая и Стюарта, невзирая на имеющиеся в ней ограничения
[11]. Исследования PPG расширили применение модели Цая и Стюарта с точностью
примерно около 5% случаев разрушения вплоть до значений приложенной нагрузки
до 41 МПа.
Лейтер, Бизон и Морган (Later, Beason, Morgan [12]) разработали новую
усовершенствованную модель, учитывающую все известные факторы влияния
на величину LR оконного стекла, включая величину максимальной нагрузки,
направление нагрузки, продолжительность нагрузки, состояние поверхности
и геометрию стеклопанели. Их модель прогноза разрушения стекла использовала
двухфакторное распределение Вейбулла [13] для учета наличия поверхностных
микротрещин существенной величины и ориентации, что при наличии напряжений
от растяжения может инициировать разрушение стекла. Два характеристических
параметра m и k для учета (по Вейбуллу) поверхностных микротрещин и царапин
были откалиброваны с учетом данных нагружения вплоть до разрушения образцов
стекла, отслуживших по 20 лет в окнах.
В то же самое время Валлабхан и Ванг (Vallabhan, Wang [14]) представили
нелинейную конечно-разностную быстросходящуюся к решению модель, сочетающую
преимущества бигармонического метода по двум осям симметрии вдоль срединной
линии прямоугольной панели. Более примечательно то, что эта конечно-разностная
модель была первой численной моделью, которая надежно прогнозировала нагрузки
в экспериментально испытываемых панелях оконного стекла. Впоследствии
модель определения разрушающих нагрузок листового стекла [12] была скомбинирована
с нелинейной конечно-разностной моделью [14], что обеспечило появление
вычислительно эффективного и быстрого численного метода определения вероятности
разрушения панели любой геометрической формы и при любом характере конструкционной
нагрузки.
В 1989 г. рабочая группа из ASTM формализовала модель прогноза разрушения
[12] в первый стандарт ASTM по расчету сопротивления нагрузке (LR) монолитного
отожженного оконного стекла. Стандарт ASTM E 1300-89 [15] и все его последующие
версии использовали номограммы рядов нормативной нагрузки (NFL) или номограммы
нагружения эквивалентной конструкции в том виде, как они были представлены
в версии 1989 г. для определения LR. Номограммы NFL соотносятся с вероятностью
разрушения 8 листов из тысячи при первом событии нагружения расчетной
конструкционной нагрузкой. Как и в предыдущих строительных нормах, эти
номограммы NFL учитывали исключительно 60-секундную продолжительность
нагружения. Различные существенные дополнения были внесены в более поздние
версии стандарта. В стандарт ASTM E 1300-94 [16] был добавлен ряд факторов
для подсчета LR для других типов стекла, включая термообработанное закаленное,
ламинированное и теплоизолирующие стеклопакеты с покрытием. В ASTM E 1300-02
[17] продолжительность нагружения была сокращена до 3 с для лучшей синхронизации
с нагружением, описанном в документе ASCE7-98 [18], первом в США стандарте
по учету ветровой нагрузки.
Рис. 1 показывает пример NFL-номограммы, подобной тем, что содержатся
в действующей версии стандарта ASTM E 1300-07 [19]. Для определения нормативной
нагрузки NFL для прямоугольной панели достаточно одной интерполяции между
линиями постоянного аспекта соотношения сторон панели и двумя восходящими
секущими линиями, которые делят кривые NFL на отрезки. Например, используя
номограмму на рис. 1, для стекла толщиной 6 мм с размерами 2000 мм и 1000
мм получим соответствующую величину нормативной нагрузки NFL примерно
около 1,9 кПа.
Линии NFL, показанные на рис. 1, с максимальной величиной менее 3 кПа
заворачиваются в обратную сторону между линиями аспекта соотношения сторон
1,5 и 3,0. Каждый из графиков NFL имеет подобный загиб линий NFL, исключая
линию с максимальным значением, поскольку он выходит за рамки номограммы.
С момента представления первоначальной версии номограмм в ASTM E1300-89
[15] не было дано никаких объяснений относительно загиба линий NFL. Вдобавок,
ни в какой из версий стандартов не было никакой дополнительной информации
касательно характера максимальной величины нагрузки на панель, соответствующей
NFL. Недостаток информации привел к появлению вопросов относительно этой
неоднозначности — загиба линий NFL и соответствующего им максимума нагрузки.
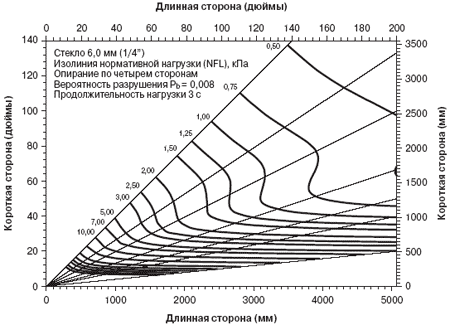
Рис. 1. Величины NFL для стекла толщиной 6,0 мм
Методика
Авторы создали ряд последовательных конфигураций остекления с учетом толщины
листов, прямоугольной поверхности и соотношения сторон для изучения зоны
обратного изгиба кривых постоянных нагрузок NFL. Наборы с разными конфигурациями
остекления состояли из 12 пластин разной толщины, соответствующей рядам
из ASTM E 1300-07 [19] — от 2,5 мм до 22 мм и комбинациями соотношений
длинной и короткой стороны от 300 мм до 5000 мм с шагом по 50 мм. Итоговые
вычисления суммировали минимально дозволенные значения толщины для каждого
номинала размера листов. Вследствие симметрии, при анализе учитывались
только комбинации соотношения длины к ширине с аспектами от 1,0 до 10,
что составило в целом 4600 конфигураций остекления для пластин с одинаковой
толщиной. Большое число испытываемых конфигураций остекления вызвало возникновение
повышенных требований к устройству испытательного контура нагружения.
Конечно-разностная модель Валлабхана и Ванга (Vallabhan, Wang [14]) с
моделью прогноза разрушающих нагрузок [12] были использованы в виде прикладной
программы вычислений нагрузок для каждой формы конфигурации при воздействии
NFL, приводящей к вероятности разрушения 8 листов из 1000. При создании
матмодели вычисления напряжений была применена разбивка сетью из 1000
узлов на каждый квадрант прямоугольной пластины. Большое число узлов служит
более точному вычислению величин напряжений и поперечных прогибов для
каждого узла. Было выбрано такое число строк и столбцов узлов, чтобы соблюсти
номинальное соответствие прямоугольных размеров и одинаковость расстояния
между узлами по осям x и y. Ось x всегда параллельна длинной стороне прямоугольника.
Для отожженного стекла были выбраны значения модуля Юнга и коэффициента
Пуассона 71,7 ГПа и 0,22, соответственно.
Используя круг напряжений Мора (Mohr’s circle), были вычислены сочетанные
максимум и минимум главных напряжений из суммы соответствующих компонент
напряженного состояния, т.е. напряжений, подобных напряжениям мембраны
и напряжениям изгиба, включая две нормальные составляющие и составляющую
от сдвига. После определения напряжений для каждого узла модели, была
рассчитана вероятность разрушения с использованием параметров m и k поверхностных
микротрещин, полученные по двухфакторному распределению Вейбулла [13]
по методике из ASTM E 1300-07 [19]. Значения для m и k в ASTM E 1300-07
[19] даны как 7 и 2,86 ? 10–53 Н–7.м12 соответственно. Общая вероятность
разрушения для стеклянной панели была вычислена путем суммирования вклада
каждого узла.
Используя графики, отформатированные подобно номограммам NFL, представленным
в ASTM E1300-07 [19], авторы создали ряды графиков, опираясь на самое
большое значение из возникающих в контуре сочетаний наибольших значений
составляющих главного напряжения (single largest combined maximum principal
stress, SLCMPS) и соответствующее ему NFL для каждой комбинации длины
и ширины прямоугольника и каждого номинала толщины листа. Вертикальная
ось представляет собой короткую сторону листа, горизонтальная ось — длинную
сторону прямоугольной пластины из стекла. Вследствие быстрого увеличения
значений SLCMPS по короткой стороне, контурные линии ограничены значением
около 40 МПа для ясности. Вместо прямоугольной сетки в качестве ссылок
были нанесены линии постоянного соотношения сторон, выражающие действие
коэффициента соотношения сторон на значения SLCMPS.
Прежде чем начать детальное описание полученных результатов для напряжений
и их соотношение с линиями постоянных значений NFL из ASTM E 1300-07 [19],
представляется полезным представить характеристики и тренды линий постоянных
NFL, показанных в номограммах из ASTM E 1300-07 [19]. На рис. 1 показаны
графики кривых постоянных значений NFL при толщине листа стекла 6 мм.
Кривые NFL явно загибаются в обратную сторону между значениями напряжений
0,75 кПа и 3,00 кПа и между линиями соотношения сторон 1,5 и 3,0. В области
между аспектом соотношения сторон 3,0 и 10,0, все кривые NFL становятся
преимущественно линейными и имеют примерно одинаковый наклон. В области
меду аспектом сторон 1,0 и 1,5 наблюдается подобный тренд, однако, как
только значения NFL увеличиваются свыше 10,0 кПа, наклон линий начинает
уменьшаться вплоть до линий, практически параллельных горизонтали.
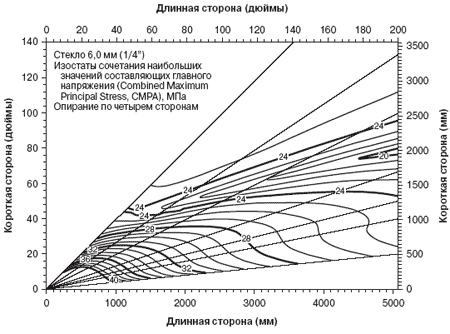
Рис. 2. Изолинии SLCMPS, соответствующие кривым NFL для стекла толщиной 6,0 мм
Результаты
Для начала объяснения взаимосвязи между данными SLCMPS и NFL полезно описать
составляющие, которые содержит в себе значение SLCMPS. Рядовая величина
SLCMPS состоит из напряжения изгиба и напряжения, подобного возникающему
в тонкой мембране, по три компоненты для каждого, которые включают в себя
две нормальные составляющие и составляющую от сдвига. Ориентация обеих
нормальных компонент напряжения (от изгиба и растяжения, подобно мембране)
определяется направлениями вдоль осей x и y соответственно. Все составляющие
напряженного состояния складываются, а для вычисления значений SLCMPS
используется круг напряжений Мора. Из-за большого числа значений толщины
пластин и, соответственно, большого числа графиков, здесь подробно обсуждаются
только результаты для стекла толщиной 6 мм. Это значение толщины на самом
деле достаточно хорошо описывает ситуацию со стеклянными панелями другой
толщины, поскольку оно находится примерно в середине диапазона исследованных
толщин, и стекло такой толщины наиболее часто применяется в строительной
отрасли. К тому же тренд, наблюдаемый на номограмме NFL (рис. 1) показал,
что эти характеристики для листа толщиной 6 мм имеют подобный характер
и для прямоугольных стекол другой толщины, т.е. следует ожидать такого
же подобия и для поведения других характеристик.
На рис. 2 представлен график SLCMPS для стекла толщиной 6,0 мм. Линии
равных напряжений, т.е. изолинии значений SLCMPS, ясно показывают наличие
относительного градиента значений SLCMPS в зависимости от соотношения
размеров прямоугольных листов.
В общем, графики показывают уменьшение значений SLCMPS при увеличении
габаритов листа, этот результат очень существенно влияет на вероятностное
распределение — при увеличении площади поверхности задействуется намного
большее число микротрещин, могущих стать причиной разрушения [12]. Для
области, где соотношение сторон находится в пределах 1,0 и 1,5 и длинная
сторона больше чем 1500 мм, значения SLCMPS уменьшаются намного медленнее.
Существенный градиент находится в области между аспектом соотношения сторон
1,5 и 4,0 и длиной короткой стороны менее 1500 мм, что соответствует т.н.
области перехода.
Далее, пластины с аспектом сторон около 2,5 имеют существенно меньшие
значения нагрузки LR, чем для других аспектов при той же самой площади
поверхности. Наличие области перехода принципиально вызвано изменением
характера напряжений с двухосного изгиба (что случается при аспектах между
1 и 1,5) на изгиб по одной оси (где значения аспекта соотношения сторон
находятся в диапазоне от 3 до 10).
Неприведенные здесь графики показывают тренды, подобные описанным выше.
У листов с толщиной менее 6,0 мм переходная область несколько сдвигается
в низ графика. Область перехода для листа толщиной 2,5 мм начинается при
значении длинной стороны приблизительно 400 мм. При увеличении толщины
листового стекла область перехода сдвигается по графику вверх вплоть до
выхода из области графика. Пластина стекла толщиной 16 мм — первое значение
толщины стекла, у которой область перехода выходит за пределы области
графика. Эта тенденция также отражена в графиках NFL в ASTM E 1300-07
[19].
Смена двухосевого изгиба на одноосевой изгиб вызывает соответствующий
изгиб линии изостаты значений NFL в графиках NFL по ASTM E 1300-07 [19].
Для лучшей иллюстрации заворота кривых NFL в области перехода нужно нарисовать
изостаты NFL из ASTM E 1300-07 [19] поверх изолиний SLCMPS для стекла
толщиной 6,0 мм, рис. 3. Для ясности, были удалены промежуточные изолинии
SLCMPS, проходящие в районе изостат NFL со значениями 4,0 кПа и 7,0 кПа.
Кривые NFL в области перехода начинают последовательно загибаться назад
при прохождении между верхней линией 24 МПа и линией 22 МПа вдоль изолиний
SLCMPS. Они не изгибаются вплоть до своего прохождения через верхний градиент
изолинии SLCMPS в области перехода и пока напряжения соответствуют условиям
изгиба вдоль одной оси. Область перехода влияет на линии NFL снижением
градуса наклона, т.е. они изгибаются тем меньше, чем более снижается градиент
изостат SLCMPS. Например, линия NFL = 0,75 кПа загибается намного сильнее
изостаты NFL = 3,0 кПа, которая почти полностью находится в области перехода.
Более того, линии NFL для значений 5 кПа и 10 кПа, которые находятся ниже
области перехода, не загибаются назад вообще. Другие графики для 11 исследованных
значений толщины стекла демонстрируют похожее поведение изолиний SLCMPS
и линий нагрузки NFL.
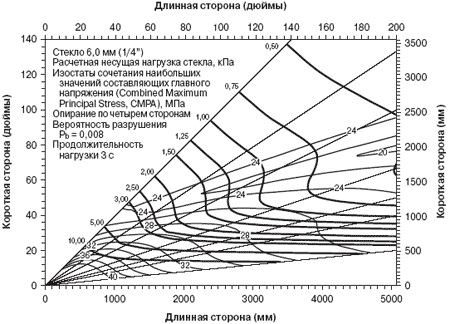
Рис. 3. Изолинии SLCMPS с наложенными соответствующими кривыми постоянных значений NFL по ASTM E 1300-07 [19] для стекла толщиной 6,0 мм
Выводы
Допустимое напряжение в конструкции обычно определяется как усилие, распределяемое
внутри материала под воздействием действующих в конструкции нагрузок,
которое в некоторых пределах меньше максимальных. С этой же целью используется
коэффициент запаса прочности в качестве подстраховки, что усилия в конструкции
будут намного ниже допустимого предела. Таким образом, если кто-то создал
метод проектирования, опирающийся на допустимых нагрузках, возникающих
в хрупком материале, подобном стеклу, то он должен сначала определиться
с верхним пределом напряжений. Однако, как указывалось ранее, разрушающее
напряжение весьма зависимо от микроизъянов на поверхности стекла, выступающих
в роли множественных концентраторов напряжений, и, таким образом, значение
напряжения существенно вариативно. Итак, можно пойти по ошибочному и консервативному
пути, выбрав напряжение несколько ниже, чем напряжение, при котором случилось
разрушение стекла. Затем коэффициентом запаса прочности еще более занизить
допустимую величину нагрузки в конструкции.
Методом численного интегрирования без особых сложностей можно подсчитать
какой-то один из известных факторов, влияющих на несущую способность стекла,
но невозможно полностью учесть действительное состояние поверхности стекла,
правильное распределение нагрузки без учета геометрии стеклянных панелей
и их толщины и способа закрепления. К тому же многие стандарты по проектированию
для других типов материалов обеспечивают схожесть подхода при проектировании
с учетом уровня допустимых напряжений в конструкции или по допустимому
уровню сопротивления нагрузке в материале, чтобы обеспечить унифицированный
подход при проектировании из разных материалов для разных типов конструкций
без учета соотношения размеров. Выбор, сделанный по любой из допустимых
нагрузок, приведет к ошибке и не позволит правильно спрогнозировать действительную
разрушающую нагрузку и согласовать данные расчета с экспериментальными
данными разрушающих усилий. Таким образом, использование в расчетах простых
однофакторных значений допустимой нагрузки приведет к ошибке при выборе
безопасной и эффективной толщины листового стекла.
Ссылки:
1. Timoshenko, S., and Woinowsky-Krieger, S. (1959). Theory of plates
and shells, McGraw-Hill Book CoМПаny, New York, 580 pp.
2. Griffith, A. A. (1920). «The phenomena of rupture and flow in solids.»
Philosophical Trans. Royal Soc., London, U.K., CCXXI(A587), 163–179.
3. Charles, R.J., (1958). «Static fatigue of glass. I,» J. of App. Phys.,
AIP, 29 (11), 1549–1553.
4. Orr, L. E. (1957). «Engineering properties of glass — Windows and glass
in the exterior of buildings.» Building Research Unit, U.S. Nat. Acad.
Sciences, Pub. 478, 51–62.
5. Bowles, R and Sugarman, B. (1962). «The strength and deflection characteristics
of large rectangular glass panels under uniform pressure.» Glass Technol.,
(3)5, 156–170.
6. Hershey, R. L, and Higgins, T. H. (1973). «Statistical prediction model
for glass breakage from nominal sonic boom loads.» NTIS Accession No.
AD-763-594, Booz-Allen Applied Research, Inc., Bethesda, Markland.
7. SBCCI. (1962). Standard building code. Birmingham, AL.
8. ICBO. (1967). Uniform building code. Whittier, CA.
9. BOCA. (1965). Basic national building code. 4th Ed., Homewood, IL.
10. Tsai, C. R., and Stewart, R. A. (1976). «Stress analysis of large
deflection of glass plates by the finite-element method.» J. Am. Ceram.
Soc., 59 (9–10), 445–448.
11. PPG. (1979). PPG glass thickness recommendations to meet architects
specified 1-minute wind load. Technical Services/Flat Glass Division,
PPG Industries, Inc., Pittsburgh, PA.
12. Beason, W.L., and Morgan, J. R. (1984). «Glass failure prediction
model.» J. Struct. Eng-ASCE., 110 (2), 197–212.
13. Weibull, W., (1939). «A statistical theory of the strength of materials,»
Handlinger NR 151, igeniorsvetenskapsakademiens (Royal Technical University),
Stockholm, Sweden.
14. Vallabhan, C. V. G., and Wang, B. Y-T. (1981). «Nonlinear analysis
of rectangular glass plates by finite difference method.» NTIS Accession
No. PB84-159649, Institute. For Disaster Research, Texas Tech University,
Lubbock, TX.
15. ASTM. (1989). «Standard practice for determining the minimum thickness
of annealed glass required to resist a specified load», ASTM E 1300-89,
West Conshohocken, PA.
16. ASTM. (1994). «Standard practice for determining the minimum thickness
and type of glass required to resist a specified load», ASTM E 1300-94,
West Conshohocken, PA.
17. ASTM. (2002). «Standard practice for determining the load resistance
of glass in buildings», ASTM E 1300-02, West Conshohocken, PA.
18. ASCE. (1998). «Minimum design loads for buildings and other structures.»
ACSE 7-98, Reston, VA.
19. ASTM. (2007). «Standard practice for determining the load resistance
of glass in buildings», ASTM E 1300-07, West Conshohocken, PA.
Д-р. Стефен М. Морзе (Stephen M. Morse), член-корреспондент
исследовательского сектора департамента гражданского и экологического
инженерного строительства Техасского технологического университета, Техас,
США, д-р Г. Скотт Норвилль (H. Scott Norville), профессор и зав.
кафедрой департамента гражданского и экологического инженерного строительства
Техасского технологического университета, Техас, США.
По материалам доклада на Glass Performance Days 2009, Тампере, Финляндия,
июнь 2009 г.