Влияние толщины и числа оборотов круглой пилы на частоты собственных колебаний
Требуемые технико-экономические показатели круглых пил в
значительной степени определяются их работоспособностью. От работоспособности
круглой пилы зависят энергозатраты, качество распиловки, потери древесины в опил.
Потеря работоспособности пильного диска связана с потерей динамической устойчивости
(изгибными колебаниями) при минимальной критической частоте вращения. Таким
образом, каждая круглая пила с заданными параметрами имеет предельно допустимую
частоту вращения. Превышение предельно допустимой частоты вращения вызывает
значительное отклонение пилы от плоского состояния, что приводит к ухудшению
качества распиловки и может вывести диск из строя. Предельно допустимая частота
вращения устанавливается частотой собственных колебаний пильного диска.
В работе определяется частота собственных поперечных колебаний пильного диска
постоянной толщины, закрепленного по внутреннему контуру планшайбой. Предполагаем,
что распределение напряжений в пиле от нагрева и центробежных сил инерции имеет
осесимметричный характер. Рассматривая малые поперечные колебания пильного диска,
пренебрегаем изменением напряжений в срединной плоскости пилы при колебаниях диска.
Дифференциальное уравнение малых поперечных колебаний пильного диска в цилиндрической
системе координат[1]:
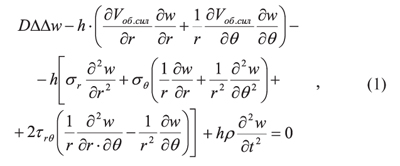
где r, θ — цилиндрические координаты;
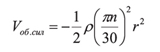
σr и σθ — нормальные компоненты напряжения
по осям r и θ;
τrθ — касательная компонента напряжения (τrθ = 0,
т.к. напряженное состояние осесимметрично);
ρ — плотность материала диска пилы;
n — число оборотов диска пилы;
t — время;
w — прогиб пластинки;
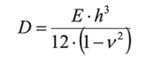
Е — модуль упругости Юнга;
h — толщина диска;
ν — коэффициент Пуассона.
При определении частот собственных колебаний диска в качестве внешних нагрузочных факторов, действующих на диск, рассматриваем центробежные и тепловые нагрузки. Напряжения от действия центробежных сил определяем по следующим зависимостям [3]:
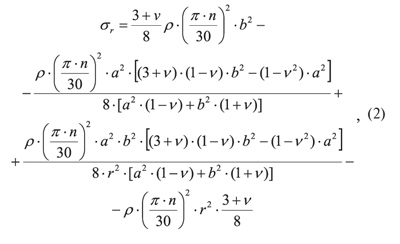
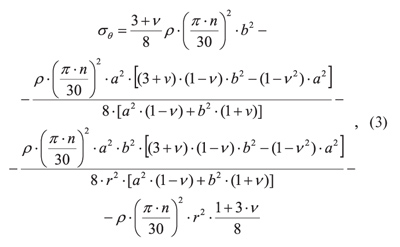
где а — радиус планшайбы;
b — радиус пильного диска.
Для определения термомеханических напряжений сперва необходимо
определить тепловое поле пильного диска.
Распределение температуры по радиусу
диска пилы описывается зависимостью [4]:
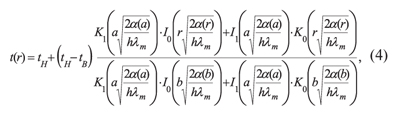
где I0, K0, I1, K1 —
функции Бесселя соответственно первого и второго рода нулевого и первого порядка
аргумента;
tВ — температура окружающей среды;
tН — температура
на наружном радиусе (b) диска;
λm — коэффициент теплопроводности
материала диска круглой пил.
Коэффициент теплоотдачи от диска воздуху α(r), определяется по формуле [4]:
где ω — угловая скорость;
с и ψ — коэффициенты, зависящие от
вида, параметров охлаждающей среды и условий охлаждения;
λf — коэффициент
теплопроводности воздуха при температуре окружающей среды;
νf — коэффициент кинематической вязкости воздуха при температуре
окружающей среды.
Напряжения, возникающие от неравномерного нагрева диска пилы, в радиальном и тангенциальном направлениях σr(r) и σθ(r) определяются по формулам [3]:
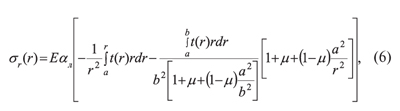
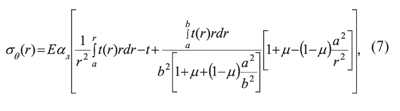
где αл — коэффициент линейного расширения материала круглой пилы.
Наиболее эффективным методом решения дифференциального уравнения (1) является приближенный метод Бубнова-Галеркина. Для приближенного решения задачи по данному методу задаемся выражением для прогиба в виде суммы конечного числа членов:
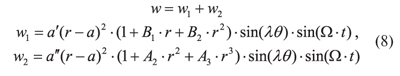
где α′, α″ — вариационные параметры;
λ — число узловых диаметров;
Ω — частота собственных колебаний диска пилы;
B1, B2, A2, A3 — безразмерные коэффициенты.
Функции (8) автоматически удовлетворяют граничным условиям на внутреннем контуре. На внутреннем радиусе диска, равном радиусу планшайбы (r = a), прогиб и угол поворота пластины равны нулю [4]:

Безразмерные коэффициенты определяются из условия, что функции (8) удовлетворяют граничным условиям на внешнем контуре [4]:
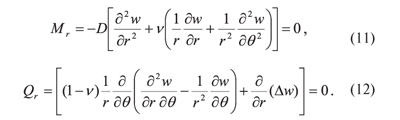
Подставляя функции (8) в дифференциальное уравнение (1), вариационное уравнение Бубнова-Галеркина примет вид:
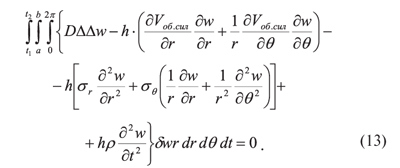
В данном вариационном уравнении за начальный момент времени примем t1 = 0, а за конечный момент времени — период рассматриваемого свободного колебания t2 = 2π /σ, тогда вариационное уравнение перепишется в виде:
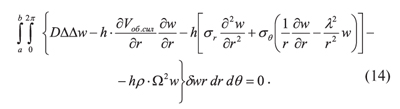
Вследствие независимости вариаций δa′ и δa″ множители при них должны обращаться в нуль. Это приводит к системе линейных уравнений относительно a′ и a″:

где
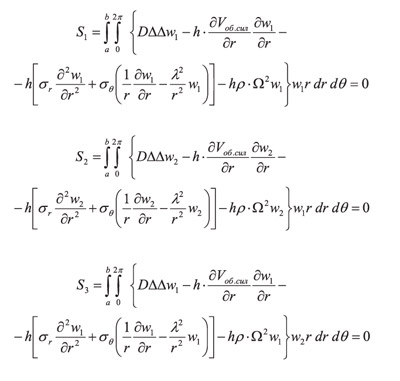
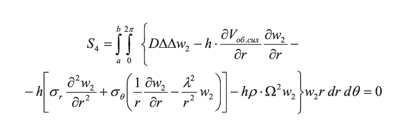
Приравнивая к нулю определитель системы (15):
находим частоту собственных колебаний пильного диска.
|
Рассмотрим пример расчета частоты собственных колебаний для
пильного диска диаметром 2b = 1000 мм, диаметром планшайбы 2a = 160 мм. В расчете
принимаем следующие параметры материала пилы (сталь 9ХФ): модуль упругости Юнга
E = 2,1.105 МПа; коэффициент Пуассона μ = 0,27; плотность материала ρ = 7850 г/см3;
коэффициент линейного расширения материала круглой пилы αл = 11,5.10–6 °C–1.
Температура окружающей среды tВ = 20°С; температура на наружном радиусе
(b) диска tН = 90°С. Коэффициенты, зависящие от вида и параметров
охлаждающей среды и условий охлаждения с = 0,0287 и ψ = 0,8; коэффициент теплопроводности
воздуха при температуре окружающей среды λf = 0,0259 Вт/(м2°С);
коэффициент теплопроводности материала диска круглой пилы λm = 44,7 Вт/(м2°С);
коэффициент кинематической вязкости воздуха при температуре окружающей среды
νf = 15,06.10–6 м2/с. Расчет ведем для дисков
толщиной от 2 мм до 5 мм с шагом 0,5 мм и числом оборотов от 750 об./мин. до
1550 об./мин. с шагом 50 об./мин. |
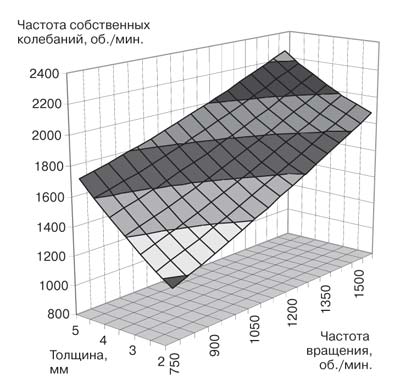
Рис. 1. Зависимость частоты собственных колебаний с одним узловым диаметром от толщины и частоты вращения пильного диска
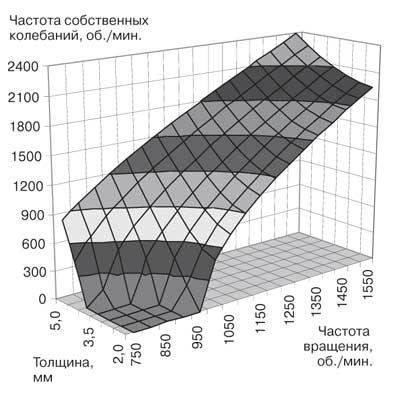
Рис. 2. Зависимость частоты собственных колебаний с двумя узловым диаметрами от толщины и частоты вращения пильного диска
Расчет пильных дисков, рассмотренных в примерах, также был
проведен с использованием метода конечных элементов в программном комплексе
ANSYS, который показал расхождение результатов не более 5%.
Максимальное число оборотов пильного диска определяется по зависимости [5]:

Таким образом, на основании представленной модели найдены зависимости частоты собственных колебаний диска пилы от его толщины и числа оборотов, используя которые, возможно определить наиболее рациональные толщину и число оборотов пильного диска с точки зрения его устойчивости.
Список использованных источников
- Жодзишский Г. А. Влияние напряжений от неравномерного нагрева, проковки и центробежных сил инерции на частоты свободных колебаний круглых пил: диссертация ... кандидата технических наук. — ЛТА, 1958.
- С. П. Тимошенко, С. Войновский-Кригер Пластинки и оболочки / пер. с англ.; под ред. Г. С. Шапиро. — Изд. 3-е, М.: Наука, 1966 — 635 с. ил, табл.; 22 см.
- Тимошенко С.П., Гудьер Дж. Теория упругости: Пер. с англ./Под ред. Г.С. Шапиро. — 2-е изд. — М.: Наука, 1979, 560 с.
- Пашков В.К. Теплофизика резания древесины круглыми пилами: монография. Екатеринбург: Урал. гос. лесотехн. ун-т, 2007,311с. ISBN 978-5-94984-144-0.
- Стахиев Ю.М. Работоспособность плоских круглых пил. — М.: Лесн. пром-сть, 1989. — 384 с. ISBN 5 — 7120 — 0197 — 7.
Власов А.В. (ВятГУ, г. Киров, РФ).
По материалам доклада
на V Международном евразийском симпозиуме «Деревообработка: технологии, оборудование,
менеджмент XXI века», г. Екатеринбург, РФ, сентябрь 2010 г.