Прочностные свойства стекла. Несущая способность. Расчет на прочность. Допустимые напряжения при изгибе
В табл. 1 приведены основные прочностные и физико-технические характеристики стекла.
Таблица 1. Прочностные и физико-технические характеристики стеклаДопустимые напряжения при изгибе
| Плотность, кг/м3 |
2500
|
| Теплопроводность, Вт/м К |
0.84
|
| Коэффициент температурного расширения, 1/°С |
6-9 х 10-6
|
| Прочность на сжатие, кН/м2 |
100 х 104
|
| Прочность на растяжение, кН/м2 (МПа) |
3-10 х 104 (30-100)
|
| Прочность на изгиб, кН/м2 (МПа) |
3-10 х 104 (30-100)
|
| Удельная теплоемкость, кДЖ/кг К |
0.84
|
| Коэффициент Пуассона |
0.25
|
| Излучательная способность, Вт/м К |
0.84
|
| Показатель преломления |
1.5
|
Допустимые напряжения при изгибе
Как видно из табл. 1, стекло имеет высокую прочность на сжатие и значительно меньшую на растяжение и изгиб. Поэтому для расчета несущей способности конструкций из стекла необходимо знать величину допустимых напряжений при изгибе, которая для стекла не является постоянной, как у многих других материалов, а изменяется по величине в зависимости от следующих факторов:
Учитывая особые свойства стекла при расчете на прочность, нагрузки
по характеру подразделяются не только по длительности действия, но и
на эксплуатационные и разрушающие. К эксплуатационным относятся: ветровая
и снеговая нагрузки, нагрузки от скопления людей и собственного веса.
К разрушающим относятся температурные и ударные: нагрузки, вызванные
различными ударами или взрывной (ударной) волной.
Стекло, испытавшее эксплуатационную нагрузку в течение длительного
времени, обладает значительно более низкой несущей способностью по сравнению
со вновь установленным стеклом. Так при расчете на кратковременные
нагрузки, к которым можно отнести ветровые, величина допустимых напряжений
при изгибе стекла может быть принята равной
60-70 МПа. А при длительных нагрузках, к которым можно отнести собственный
вес, это значение следует принимать равным приблизительно 30 МПа.
Величина допустимого напряжения может быть выбрана из таблиц или графиков
в соответствии с Рис. 1 в зависимости от вида нагрузки, способа крепления
и соотношения сторон.
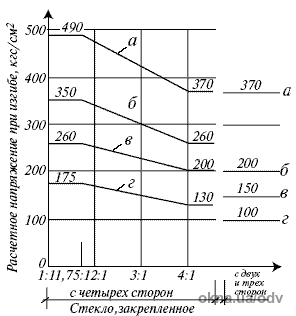
Рис. 1. Допустимые напряжения при изгибе, принимаемые в расчетах:
а) закаленного стекла;
б) обычного оконного стекла при действии ветровой нагрузки;
в) оконного стекла при действии ветровой и снеговой нагрузки, нагрузки
от скопления людей и собственного веса;
г) обычного оконного стекла, установленного в фонарях (или кровлях)
при действии снеговой нагрузки от собственного веса и скопления людей.
Из Рис. 1 хорошо видно, что на несущую способность стекла оказывают влияние такие факторы, как способ его крепления и соотношение сторон (при четырехстороннем закреплении).
Таблица 2.
Допустимые расчетные напряжения при изгибе для стекла при различных
значениях запаса прочности. (По данным Инженерного бюро Аулис Бертин
— Финляндия)
|
Коэффициент запаса прочности
|
Допустимое расчетное напряжение при изгибе,
МПа
|
|
|
Ламинированное/обычное стекло
|
Закаленное стекло
|
|
|
1.0
|
75
|
175
|
|
1.5
|
50
|
117
|
|
2.0
|
38
|
88
|
|
2.5
|
30
|
70
|
|
3.0
|
25
|
58
|
|
5.0
|
15
|
35
|
|
10.0
|
8
|
18
|
Допустимые напряжения при изгибе могут быть также определены на основе
расчетных напряжений в момент разрушения с учетом коэффициента запаса
прочности, величина которого зависит от вида нагрузки, способа закрепления
стекла и соотношения сторон. На основании значений разрушающей нагрузки,
задаваемой опытным путем (до момента, когда 95 % стекол выдерживают
ее), рассчитываются напряжения в момент разрушения. В табл. 2 приведены
значения допустимых напряжений при изгибе и коэффициентов запаса прочности
для обычных, ламинированных и закаленных стекол.
Коэффициент запаса прочности выбирается на основании функционального
назначения здания с учетом эксплуатационных факторов неопределенности
и риска. Запас прочности закаленных стекол, как правило, принимается
ниже, чем у обычных.
В качестве ориентировочной величины при предварительных расчетах возможно
принимать допустимые напряжения при изгибе стекла sдоп = 25 МПа.
Расчет стеклянных пластин на эксплуатационные нагрузки
из условий прочности и жесткости
С точки зрения теории упругости стекло представляет собой тонкую плоскую
пластину. Линейная теория расчета пластин исходит из того, что их прогиб
не превышает толщины. При расчете стекол, которые прогибаются незначительно,
используют дифференциальное уравнение, которое в литературу о стекле
вошло под названием формулы Баха. Его решение для расчета оконных стекол
на ветровую нагрузку не представляет особой трудности.
Однако прогиб больших оконных стекол под нагрузкой может быть в несколько
раз больше их толщины. При этом плоская пластина превращается в пространственную
оболочку, где кроме изгибных возникают и мембранные напряжения, а простое
дифференциальное уравнение переходит в систему дифференциальных уравнений
в частных производных, решение которого значительно сложнее. Соотношение
изгибных и мембранных напряжений, возникающих в балке при различных
ее прогибах, показано на Рис. 2.
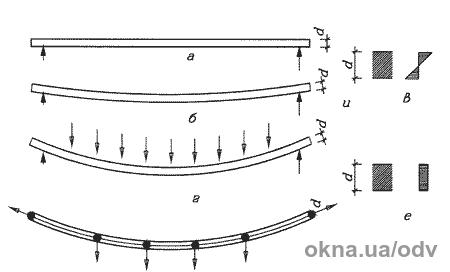
Рис. 2. Соотношение изгибных и мембранных напряжений, возникающих
в балке при различных ее прогибах:
а) балка без нагрузки;
б) балка под нагрузкой с небольшим прогибом;
в) эпюра изгибных напряжений в балке с небольшим прогибом;
г) балка со значительным прогибом при увеличении нагрузки;
д) направления растягивающих усилий в балке со значительным прогибом;
е) эпюра мембранных напряжений в балке со значительным прогибом
Вертикальные конструкции из стекла
В теории расчета стекол вертикально расположенным считается стекло,
отклонение которого от вертикальной плоскости не превышает 10°,
а отклонение верхнего края от вертикальной плоскости, проходящей через
нижний край, не более 300 мм. Толщина одинарной пластины в вертикально
расположенном окне при равномерно распределенной нагрузке определяется
с помощью формулы Маркуса:
где t — толщина стеклянной пластины [мм];
ss — допустимое расчетное напряжение;
р — полная ветровая нагрузка на стеклянную пластину [кН];
r — соотношение сторон b/а; где b — более короткая сторона;
u — коэффициент Пyaccoнa (для стекла 0.25).
| Соотношение сторон а/b |
1,0
|
1,1
|
1,2
|
1,3
|
1,4
|
1,5
|
1,6
|
1,7
|
1,8
|
1,9
|
2,0
|
3,0
|
4,0
|
5,0
|
| Коэффициент формы |
0,28
|
0,33
|
0,37
|
0,41
|
0,45
|
0,48
|
0,51
|
0,54
|
0,56
|
0,59
|
0,61
|
0,71
|
0,74
|
0,75
|
Наклонные конструкции из стекла; конструкции стеклянных
крыш
На стекла, установленные в крышах, действуют как кратковременные ветровые,
так и долговременные снеговые нагрузки и собственный вес стеклянной
пластины. Для учета различной величины силы, вызывающей долго- и кратковременные
нагрузки, вводится коэффициент. Коэффициент 2,6 в формуле (3) используется
для долговременно влияющей нагрузки. Толщина стекол определяется по
методу Тимошенко, причем предполагается, что: 1) стеклянная плита не
претерпевает никаких горизонтальных перемещений и 2) стеклянная плита
равномерно опирается на четыре стороны
t — толщина стеклянной пластины [мм];
qd — суммарная расчетная нагрузка, [Н/м2];
b — более короткая сторона стеклянной пластины, [м];
b — коэффициент, учитывающий форму пластины (табл. 3);
s — допустимые расчетные напряжения (график Рис. 1).
2.6 — коэффициент, учитывающий долговременную нагрузку для стеклянных
пластин;
a — угол отклонения стеклянной крыши от вертикали;
q — собственный вес стеклянной крыши, [Н/м2];
q0 — снеговая нагрузка, [Н/м2];
mk — коэффициент формы при расчете снеговой нагрузки;
(СНиП “Нагрузки и воздействия”)
qk — ветровая нагрузка [Н/м2];
m — коэффициент формы при расчете ветровой нагрузки
(СНиП “Нагрузки и воздействия”)
Сосредоточенная нагрузка, действующая на стеклянную
пластину кровли
Возможные сосредоточенные нагрузки не рассматриваются одновременно с
существующей снеговой нагрузкой. Расчетная толщина стеклянной пластины,
загруженной сосредоточенной нагрузкой, определяется с помощью формулы:
b — коэффициент, учитывающий форму пластины (табл. 3);
q — собственный вес стеклянной крыши, [Н/м2];
k — коэффициент эффективного сечения (табл. 4).
Под сосредоточенной понимается нагрузка, действующая в пределах площади
100 мм і 100 мм (Рис. 3).
Соотношение области влияния сосредоточенной нагрузки и размера плиты
учитывается с помощью коэффициента k (табл. 4).
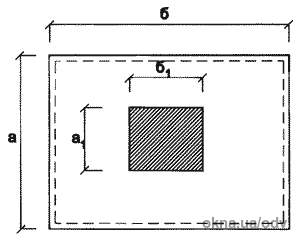
Рис. 3. Схема к расчету на действие сосредоточенной нагрузки
Табл. 4. Значения коэффициента, зависящего от соотношения площади влияния сосредоточенной нагрузки и размера стеклянной плиты кровли
|
а1/a или b1/b
|
k
|
|
1,0
|
1,00
|
|
0,5
|
2,46
|
|
0,2
|
4,44
|
|
0,1
|
5,93
|
|
0,025
|
9,03
|
В некоторых случаях также применяют для определения толщины стеклянной пластины кровли упрощенную формулу Вигена:
Определение прогиба стеклянной пластины при равномерно распределенной
нагрузке
и при сосредоточенной нагрузке
Определение прогиба в средней точке стеклянной пластины, нагруженной
равномерно и свободно поддерживаемой с четырех сторон, выполняется по
формуле:
f — величина прогиба в средней точке стеклянной пластины [м];
q — нагрузка, направленная на пластину [кН/м2];
Е — коэффициент упругости (для стекла 75 .1010 Па);
b1 — коэффициент, учитывающий размеры;
b — более короткая сторона стеклянной пластины, [м].
Определение коэффициента b1, учитывающего соотношение размеров и способ
крепления, — это математическое действие, требующее точного расчета.
Достаточная точность достигается при использовании значений, взятых
из следующих схем.
Прогиб в средней точке стеклянной пластины, свободно поддерживаемой
с четырех сторон, под действием сосредоточенной нагрузки, определяется
по следующей формуле:
f — величина прогиба в средней точке стеклянной пластины, [м];
b2 — коэффициент, учитывающий размеры;
F — сосредоточенная нагрузка, направленная на пластину [Н]
b — более короткая сторона стеклянной пластины, [м].
На Рис. 4 приведены графики для определения значений коэффициентов для
стеклянной пластины, свободно закрепленной с четырех сторон:
b1 — для равномерно распределенной нагрузки, b2 — для сосредоточенной
нагрузки.
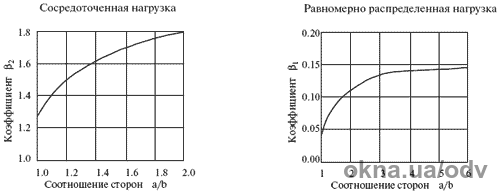
Рис. 4. Графики для определения значений коэффициентов для стеклянной
пластины, свободно закрепленной с четырех сторон:
b1 — для равномерно распределенной нагрузки, b2 — для сосредоточенной
нагрузки.
Расчет изменения длины стекла при прогибе
Чтобы определить, насколько изменяется длина прогибающегося стекла,
приведем следующий примерный расчет. Геометрические характеристики изогнутого
стекла представлены на Рис. 5
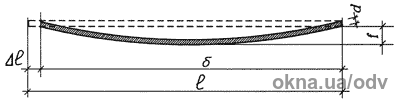
Рис. 5. Геометрические характеристики стекла при изгибе
Если представить линию прогиба изогнутого стекла в виде параболы, то, согласно Рис. 5, можно определить длину изогнутого стекла:
где I — исходная длина стекла;
s — укороченная длина стекла в проекции вследствие прогиба;
f — величина прогиба изогнутого стекла.
Уменьшение длины в этом случае составит в проекции:
И.В. Борискина, А.А. Плотников, А.В. Захаров,
“Проектирование современных оконных систем гражданских зданий”




С уважением, Зубков В.А.