Міцність скла. Несуча здатність. Розрахунок на міцність. Допустимі напруження при згині

У табл. 1 наведені основні характеристики міцності та фізико-технічні характеристики          скло.

Таблиця 1. Характеристики міцності і фізико-технічні характеристики          скла
Допустимі напруження при згині

Густина, кг/м3	2500
Теплопровідність, Вт/м К	0.84
Коефіцієнт температурного розширення, 1/°С	6-9 х 10-6
Міцність на стискання, кН/м2	100 х 104
Міцність на розтяг, кН/м2 (МПа)	3-10 х 104 (30-100)
Міцність на вигин, кН/м2 (МПа)	3-10 х 104 (30-100)
Питома теплоємність, кДЖ/кг К	0.84
Коефіцієнт Пуассона	0.25
Випромінювальна здатність, Вт/м К	0.84
Показник заломлення	1.5

Допустимі напруження при згині

Як видно з табл. 1, скло має високу міцність на стиск і значно          меншу на розтягання і вигин. Тому для розрахунку несучої здатності          конструкцій зі скла необхідно знати величину допустимих напружень          при вигині, яка для скла не є постійною, як у багатьох інших          матеріалів, а змінюється за величиною в залежності від наступних факторів:

• тривалості дії навантаження;
• схеми обпирання скла: по контуру з 4-х сторін, або з 2-х (3-х) сторін;
• жорсткості його закріплення на опорі;
• співвідношення довжини і ширини скла.

З огляду на особливі властивості скла при розрахунку на міцність, навантаження            за характером поділяються не лише за тривалістю дії, а й            на експлуатаційні та руйнуючі. До експлуатаційних відносяться: вітрове            і снігове навантаження, навантаження від скупчення людей і власної ваги.            До руйнівних відносяться температурні і ударні: навантаження, викликані            різними ударами або вибуховою (ударною) хвилею.
Скло, що відчуло експлуатаційне навантаження протягом тривалого            часу, володіє значно більш низькою несучою здатністю в порівнянні            зі знову встановленим склом. Так при розрахунку на короткочасні            навантаження, до яких можна віднести вітрові, величина допустимих напружень            при вигині скла може бути прийнята рівною
           60-70 МПа. А при тривалих навантаженнях, до яких можна віднести власну            вагу, це значення слід приймати рівним приблизно 30 МПа.
Величина допустимої напруги може бути обрана з таблиць або графіків            відповідно до Рис. 1 у залежності від виду навантаження, способу кріплення            і співвідношення сторін.

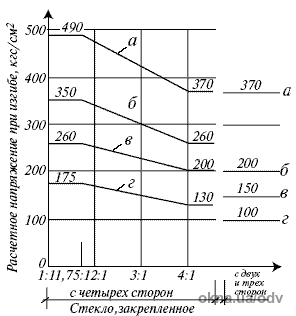
Рис. 1. Допустимі напруження при згині, що приймаються в розрахунках:
а)загартованого скла;
б) звичайного віконного скла при дії вітрового навантаження;
в) віконного скла при дії вітрового і снігового навантаження, навантаження            від скупчення людей і власної ваги;
г) звичайного віконного скла, встановленого в ліхтарях (або покрівлях)            при дії снігового навантаження від власної ваги і скупчення людей.

Із Рис. 1 добре видно, що на несучу здатність скла надають            вплив такі чинники, як спосіб його кріплення і співвідношення сторін            (при чотирибічному закріпленні).

Таблиця 2.
Допустимі розрахункові напруги при вигині для скла при різних            значеннях запасу міцності. (За даними Інженерного бюро Ауліс Бертін            - Фінляндія)

Коефіцієнт запасу міцності	Допустиме розрахункове напруження при згині, МПа
	Ламіноване / звичайне скло	Загартоване скло
1.0	75	175
1.5	50	117
2.0	38	88
2.5	30	70
3.0	25	58
5.0	15	35
10.0	8	18

Допустимі напруги при вигині можуть бути також визначені на основі           розрахункових напружень у момент руйнування з урахуванням коефіцієнту запасу           міцності, величина якого залежить від виду навантаження, способу закріплення           скла і співвідношення сторін. На підставі значень руйнівного навантаження,           задається дослідним шляхом (до моменту, коли 95% скла витримують           її), розраховуються напруги в момент руйнування. У табл. 2 наведені           значення допустимих напружень при згині і коефіцієнтів запасу міцності           для звичайного, ламінованого і загартованого скла.
Коефіцієнт запасу міцності вибирається на підставі функціонального            призначення будівлі з урахуванням експлуатаційних факторів невизначеності            і ризику. Запас міцності загартованого скла, як правило, приймається            нижче, ніж у звичайного.
У якості орієнтовної величини при попередніх розрахунках можливо            приймати допустимі напруження при згині скла sдоп = 25 МПа.

Розрахунок скляних пластин на експлуатаційні навантаження            з умов міцності і жорсткості
Із точки зору теорії пружності скло являє собою тонку плоску            пластину. Лінійна теорія розрахунку пластин виходить із того, що їх прогин            не перевищує товщини. При розрахунку скла, яке прогинається незначно,            використовують диференціальне рівняння, яке в літературу про скло            увійшло під назвою формули Баха. Його рішення для розрахунку шибок            на вітрове навантаження не представляє особливих труднощів.
Однак прогин великих шибок під навантаженням може бути в кілька            раз більше їх товщини. При цьому плоска пластина перетворюється в просторову            оболонку, де крім вигинних виникають і мембранні напруги, а просте            диференціальне рівняння переходить у систему диференціальних рівнянь            у приватних похідних, рішення якого значно складніше. Співвідношення            вигинистих і мембранних напружень, що виникають у балці при різних            її прогинах, показано на Рис. 2.

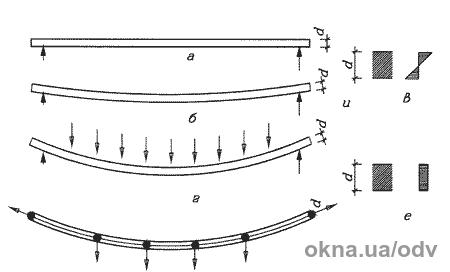
Рис. 2.Співвідношення вигинистих і мембранних напружень, що виникають            у балці при різних її прогинах:
а) балка без навантаження;
б) балка під навантаженням із невеликим прогином;
в) епюра згинальних напружень у балці з невеликим прогином;
г) балка зі значним прогином при збільшенні навантаження;
д) напрямки розтягуючих зусиль у балці зі значним прогином;
е) епюра мембранних напружень у балці зі значним прогином

Вертикальні конструкції зі скла
У теорії розрахунку скла вертикально розташованим вважається скло,            відхилення якого від вертикальній площині не перевищує 10°,
а відхилення верхнього краю від вертикальної площини, що проходить через            нижній край, не більше 300 мм. Товщина одинарної пластини в вертикально            розташованому вікні при рівномірно розподіленому навантаженні визначається            за допомогою формули Маркуса:

де t — товщина скляної пластини [мм];
ss — допустиме розрахункове напруження;
р — повне вітрове навантаження на скляну пластину [кН];
r — співвідношення сторін b/а; де b — коротша сторона;
u — коефіцієнт Пуассона (для скла 0.25).

Таблиця 3. Коефіцієнт, що враховує форму скляної пластини

Співвідношення сторін а/b	1,0	1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9	2,0	3,0	4,0	5,0
Коефіцієнт форми	0,28	0,33	0,37	0,41	0,45	0,48	0,51	0,54	0,56	0,59	0,61	0,71	0,74	0,75

Похилі конструкції зі скла; конструкції скляних            дахів
На склі, встановленому в дахах, діють як короткочасні вітрові,           так і довготривалі снігові навантаження і власна вага скляної           пластини. Для обліку різної величини сили, що викликає довго- і короткочасні           навантаження, вводиться коефіцієнт. Коефіцієнт 2,6 у формулі (3) використовується           для довготривало впливу навантаження. Товщина скла визначається по           методу Тимошенко, причому передбачається, що: 1) скляна плита не           зазнає ніяких горизонтальних переміщень і 2) скляна плита           рівномірно спирається на чотири сторони

t — товщина скляної пластини [мм];
q_d — сумарне розрахункове навантаження, [Н/м²];
b — коротша сторона скляної пластини, [м];
b — коефіцієнт, що враховує форму пластини (табл. 3);
s — допустимі розрахункові напруги (графік Рис. 1).

2.6 —коефіцієнт, що враховує довготривале навантаження для скляних            пластин;
a — кут відхилення скляного даху від вертикалі;
q — власна вага скляного даху, [Н/м²];
q₀ — снігове навантаження, [Н/м²];
m_k — коефіцієнт форми при розрахунку снігового навантаження;
(СНіП “Навантаження і впливи”)
q_k — вітрове навантаження [Н/м²];
m — коефіцієнт форми при розрахунку вітрового навантаження
(СНиП “Навантаження і впливи”)

Зосереджене навантаження, яке діє на скляну            пластину покрівлі
Можливі зосереджені навантаження не розглядаються одночасно з            існуючими сніговим навантаженнями. Розрахункова товщина скляної пластини,            завантаженої зосередженим навантаженням, визначається за допомогою формули:

b — коефіцієнт, що враховує форму пластини (табл. 3);
q — власна вага скляного даху, [Н/м²];
k — коефіцієнт ефективного перетину (табл. 4).
Під зосередженою розуміється навантаження, яке діє в межах площі 100 мм і 100 мм (Рис. 3).
Співвідношення області впливу зосередженого навантаження і розміру плити            враховується за допомогою коефіцієнту k (табл. 4).

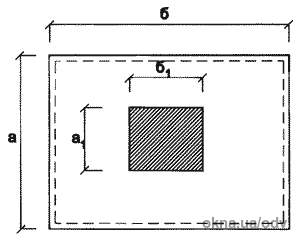
Рис. 3. Схема до розрахунку на дію зосередженого навантаження

Табл. 4. Значення коефіцієнта, що залежить від співвідношення площі            впливу зосередженого навантаження і розміру скляної плити покрівлі

а1/a чи b1/b	k
1,0	1,00
0,5	2,46
0,2	4,44
0,1	5,93
0,025	9,03

У деяких випадках також застосовують для визначення товщини скляної            пластини покрівлі спрощену формулу Вігена:

Визначення прогину скляної пластини при рівномірно розподіленим            навантаженням
і при зосередженому навантаженні
Визначення прогину в середній точці скляної пластини, навантаженої            рівномірно і вільно підтримуваної з чотирьох сторін, виконується за            формулою:

f — величина прогину в середній точці скляної пластини [м];
q — навантаження, спрямоване на пластину [кН/м²];
Е — коефіцієнт пружності (для скла 75 .1010 Па);
b1 — коефіцієнт, що враховує розміри;
b — коротша сторона скляної пластини, [м].

Визначення коефіцієнта b1, що враховує співвідношення розмірів і спосіб            кріплення, - це математична дія, що вимагає точного розрахунку.            Достатня точність досягається при використанні значень, узятих            із наступних схем.
Прогин у середній точці скляної пластини, вільно підтримуваної            з чотирьох сторін, під дією зосередженого навантаження, визначається            за такою формулою:

f — величина прогину в середній точці скляної пластини, [м];
b2 — коефіцієнт, що враховує розміри;
F — зосереджене навантаження, спрямоване на пластину [Н]
b — коротша сторона скляної пластини, [м].
На Рис. 4 наведені графіки для визначення значень коефіцієнтів для            скляної пластини, вільно закріпленої з чотирьох сторін:
b1 — для рівномірно розподіленого навантаження, b2 - для зосередженого            навантаження.

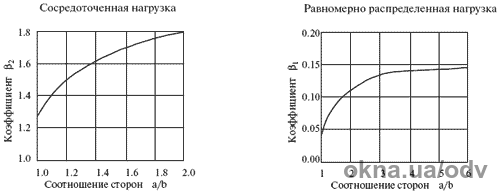
Рис. 4. Графіки для визначення значень коефіцієнтів для скляної            пластини, вільно закріпленої з чотирьох сторін:
b1 — для рівномірно розподіленого навантаження, b2 - для зосередженого            навантаження.

Розрахунок зміни довжини скла при прогині
Щоб визначити, наскільки змінюється довжина прогину скла,            наведемо наступний приблизний розрахунок. Геометричні характеристики вигнутого            скла представлені на Рис. 5

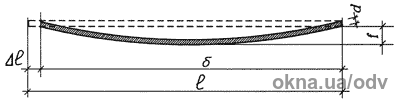
Рис. 5. Геометричні характеристики скла при вигині

Якщо уявити лінію прогину вигнутого скла у вигляді параболи, то,            згідно Рис. 5, можна визначити довжину вигнутого скла:

де I — вихідна довжина скла;
s — укорочена довжина скла в проекції внаслідок прогину;
f — величина прогину вигнутого скла.
Зменшення довжини в цьому випадку складе в проекції:

---

І.В. Боріскіна, О.О. Плотніков, О.В. Захаров,
“Проектування сучасних віконних систем цивільних будівель”