Возможности совершенствования тепловой обработки древесины на основе критерия жесткости

Разработанная Б. С. Чудиновым теория тепловой обработки древесины позволяет решить многие задачи технологического характера [1], но существует необходимость повышения точности расчетов по расходу тепловой энергии на данные операции и для оперативного контроля состояния древесины.
Пока можно утверждать, что точность расчетов по теплообменным процессам не слишком высока и находится в пределах до ±15%. Столь значительный диапазон изменчивости обусловлен неоднородностью физико-механических показателей древесины, которая зависит от многочисленных и часто не поддающихся контролю факторов.
Расчеты по определению потребления тепловой энергии на обработку древесины связаны с ее теплофизическими свойствами, которые опосредованно выражены коэффициентами теплоемкости (С), теплопроводности (l) и температуропроводности (a).
Значения коэффициентов l и a принимаются с учетом направления теплового потока, доли поздней древесины в общей массе, наличия сердцевинных лучей. В связи с неопределенностью и сложностью количественной оценки этих факторов установить величины тепловых коэффициентов с высокой степенью точности часто не удается или даже невозможно. Если изменения физико-механических свойств при тепловой обработке древесины выразить через некую адекватную средневзвешенную величину, то все возникающие проявления будут учтены в совокупности. По нашему мнению, этой величиной может быть критерий жесткости древесины, который определяется из выражения:

, (1)
где КЖ — безразмерная величина жесткости;
o — объемная твердость древесины, кН/м3;
y — плотность древесины, кН/м3.
Выбор такого подхода подтверждается следующим.
По исследованиям Волынского В. Н. [2] очень тесная взаимосвязь наблюдается между твердостью и плотностью древесины любых пород (коэффициент корреляции до 0,954). Это дает возможность сократить изменчивость коэффициента КЖ по твердости и плотности до ±5%.
Поскольку на практике разрезов, абсолютно ориентированных по направлению волокон древесины, не существует, то нет и необходимости учитывать разные направления воздействия теплового потока на обработанный материал. Тем не менее, при решении задач по тепловым процессам исследователи зачастую сталкиваются с большим числом переменных факторов, в результате чего оказывается невозможно вскрыть закономерности того или иного теплообменного явления.
Как известно, в теории теплопередачи применяют безразмерные теплофизические комплексы, называемые критериями теплового подобия. Эти критерии могут быть применены и для математического описания процессов гидротермической обработки.
В этом случае теплообменный критерий Фурье F0 выражается формулой:

(2)

Он определяет связь между скоростью изменения температурного поля в твердом теле, его физическими характеристиками и размерами.
Другим равноценным критерием, полученным в данной работе, является показатель жесткости древесины, который связан с ее физическими характеристиками.

(3)

где o— объемная твердость древесины, кН/м3, которая определяется по формуле:

(4)

где p — сила, действующая на образец при определении объемной твердости, кН.

Этот критерий также может быть применен для определения степени сопротивления древесины тепловому воздействию. В окончательном виде критерий жесткости выражается формулой:

(5)

Отсюда следует, что критерии F0 и КЖ по своим физическим характеристикам адекватны. Это позволяет решить некоторые задачи, связанные с расчетом тепловых процессов гидротермической обработки и определением тепловых коэффициентов для древесных материалов. После преобразований тождественного выражения критериев выявляется формула определения коэффициента температуропроводности a

, (6)

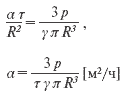
На основании оценки жесткости древесины можно с достаточно высокой степенью точности определить коэффициент температуропроводности расчетным методом и, следовательно, назначить наиболее приемлемые для конкретных условий производства параметры технологического процесса тепловой обработки.
Исследования, проведенные при получении строганого шпона, показали, что пластические свойства древесины в результате ее прогрева от 0°С до 100°С существенно изменяются. При этом модуль упругости сокращается на величину 0,93.104 МПа, а именно, с 1,34.104 МПа до 0,41.104 МПа. Исходя из предположения, что эластичность будет изменяться по такой же закономерности, что и модуль упругости, примем соотношение:

(7)

где o — объемная твердость древесины, кН/м3;
y — плотность древесины, кН/м;
К — коэффициент перевода жесткости (показатель эластичности) древесины, К = 9,3.
Введенный в формулу коэффициент означает, что для уменьшения жесткости древесины на единицу на нее оказывается тепловое воздействие, эквивалентное давлению в 9,3 кН/см2.

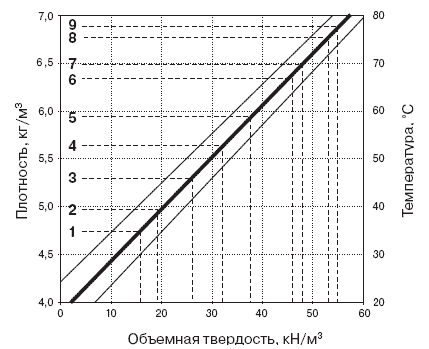
Рис. 1. Номограмма для определения оптимальной температуры нагрева на оси сортимента в зависимости от породы древесины: 1 — ель, кедр; 2— липа; 3 — сосна, осина; 4 — ольха; 5 — береза; 6 — вяз; 7 — бук; 8 — дуб; 9 — ясень

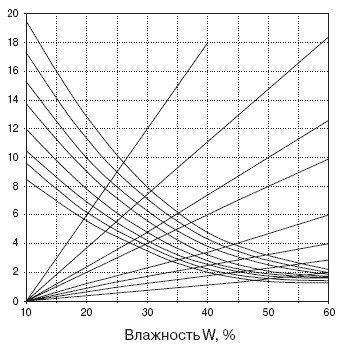
Рис.2. Номограмма для определения соотношения между характеристиками состояния древесины в условиях прогрева

Пользуясь этой формулой, была составлена номограмма (рис.1) зависимости оптимальной температуры нагрева для некоторых пород древесины перед строганием (лущением) от ее жесткости. При этом плотность древесины определялась по формуле:

(8)

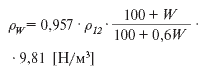
Благодаря введению нового понятия безразмерной величины жесткости и на основании проведенных исследований на древесине лиственницы, березы, ясеня составлены режимы гидротермической обработки брусьев в насыщенном паре при температуре 100°С для 12 пород древесины.
Пример определения оптимальной температуры для сосны показан стрелками и составляет 40°С. Под оптимальной температурой понимается температура, при которой эластичность периферийных и центральных зон имеет одинаковые значения и обеспечивает наиболее высокое качество строгания.
На рис. 2 приводится номограмма для определения коэффициента температуропроводности в зависимости от коэффициента жесткости древесины, ее влажности и температуры прогрева. Коэффициент температуропроводности является основным параметром, который используется при определении режима прогрева древесины.
Таким образом, при определенных параметрах тепловой обработки, в частности при оптимальной температуре для каждой породы, можно достичь увеличения скорости и снижения усилий строгания, что безусловно повышает качество механической обработки древесины.

Литература
1. Чудинов Б.С. Теория тепловой обработки древесины. Наука. — М. — 1968. — 255 с.
2. Волынский В.Н. Взаимосвязь показателей чистой древесины. Архангельский АГТУ. — 2005.

---