Модели влагопереноса внутри древесины
Свойства древесины и ее взаимодействие с водой определяются химическим
составом древесного вещества, тонкой структурой клеточных стенок, строением
и пространственным расположением отдельных анатомических элементов, из
которых построена древесина, и их совокупностей, а также связью между
ними [1–4].
Ряд ученых (П.Н. Одинцов, П.П. Эриньш [5], Н.Н. Федякин, Б.С. Чудинов
[6], A.J. Stamm, W.E. Smith [7] и др.) являются сторонниками коллоидной
природы влажных клеточных стенок древесины и при этом считают, что основным
носителем сорбционных свойств древесины является система так называемых
«непостоянных» капилляров клеточных стенок, обладающая во много раз большей
удельной поверхностью, чем постоянные капилляры.
При увлажнении их размеры увеличиваются, приобретая максимальную величину
при влажности вблизи предела насыщения клеточных стенок. При десорбции
воды непостоянные капилляры в клеточных стенках не опустошаются, а постепенно
суживаются до их полного исчезновения в абсолютно сухом состоянии.
При анализе процессов взаимодействия древесины с водой Б.С. Чудинов [6]
предложил ряд моделей пористой структуры древесины с постоянными капиллярами
различной формы сечения. Однако моделей клеточной стенки с учетом ее коллоидной
природы предложено не было. Следовательно, необходимость разработки такой
модели очевидна.
В основу модели коллоидной капиллярно-пористой структуры древесины положены
следующие принципы:
1. Свободная влага располагается в системе макрокапилляров, а связанная
— в системе непостоянных микрокапилляров.
2. Система макрокапилляров древесины моделируется следующими анатомическими
элементами:
? хвойные породы — ранние и поздние трахеиды;
? лиственные породы — сосуды (с учетом сердцевинных лучей) и древесные
волокна.
3. Система непостоянных микрокапилляров представляет собой совокупность
отверстий цилиндрической формы в клеточных стенках древесины, радиус которых
функционально зависит от влажности древесины в гигроскопической области:
rk = –8,2.10–6W4 + 5,537.10–4W3 –
– 0,013W2 + 0,159W, нм (1)
где W — влажность древесины, %.
4. К допущениям при моделировании относится то, что пористость клеточной
стенки непропорциональна базовой плотности древесины.
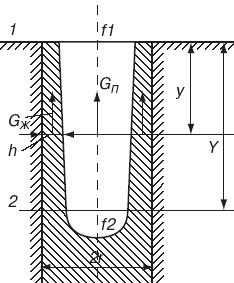
Рис. 1.
Физическая модель распределения жидкой фазы в древесном капилляре
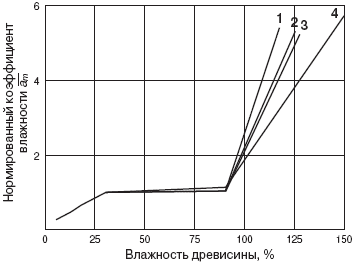
Рис. 2. Зависимость нормированного коэффициента влагопроводности от влажности древесины:
1 — лиственница; 2 — дуб; 3 — береза; 4 — сосна
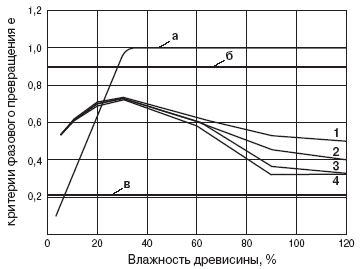
Рис. 3. Зависимость критерия фазового превращения от влажности древесины:
1 — дуб; 2 — береза; 3 — лиственница; 4 — сосна
а — данные W. Wissmann [9]; б — данные В.В. Сергеева [11];
в — данные А.В. Лыкова и Ю.А. Михайлова [12]
Результатами расчета является определение следующих параметров модели
для четырех пород древесины (сосна, лиственница, береза, дуб):
? внутренняя поверхность (для систем макро- и микрокапилляров);
? объем капилляров (для каждой из систем и суммарный);
? пористость;
? максимальная влажность.
Анализ расчетных параметров моделей позволяет сделать следующие выводы:
1. Структура моделей позволяет охватывать широкий диапазон влажности древесины,
от 5 до 120–160%.
2. Пористость древесины на моделях на 7–11 % меньше, чем по различным
экспериментальным данным, приводимым в литературе [1–4], однако это не
снижает достоверность моделирования.
3. Модели пригодны для аналитического определения параметров массопереноса
для древесины различных пород.
Для капиллярно-пористых тел, каким является древесина, влагообмен со средой
происходит за счет удаления жидкости из капилляров, выходящих на поверхность.
При равновесии жидкости в капилляре над ее мениском на стенке образуется
полимолекулярная пленка с толщиной, уменьшающейся вверх по определенному
закону, который может быть найден, если известно расклинивающее давление
П или насыщенность пара ? пленки в функции ее толщины h (рис. 1).
Если парциальное давление паров жидкости отличается от того, которое отвечает
равновесию жидкости с мениском в капилляре, то будет идти либо испарение,
либо конденсация на мениске.
Если радиус капилляра r не более 10–5 м, то скорость этого процесса определяется
не только потоком диффузии пара через газ, но и потоком, переносимым пленкой
влаги, при ее течении под влиянием градиента толщины h. Для оценки вклада
пленочного механизма было использовано уравнение Дерягина-Нерпина.
Из условия стационарности процесса следует, что суммарная скорость испарения
G равна
G = GП + GЖ , (2)
где GП — поток пара;
GЖ — поток жидкости в пленке.
Используя преобразования Н.В. Чураева [8], были получены расчетные формулы
для определения GП и GЖ для случая полного смачивания стенок капилляра
водой и без учета возможного влияния термовлагопроводности.
В результате проведенных последующих вычислений и их анализа получены
следующие результаты.
На рис. 2 приведены значения нормированного коэффициента влагопроводности
для различных пород древесины в функции влажности, описываемые следующими
уравнениями регрессии:
Сосна:
a–m = –1,695.10–9W5 + 5,775.10–7W4 – 6,057.10–5W3 +
+ 2,063.10–3W2 + 5,764.10–3W + 0,169 (3)
Лиственница:
a–m = –3,362.10–11W5 + 2,43.10–7W4 – 3,786.10–5W3 +
+ 1,429.10–3W2 + 0,013W + 0,146 (4)
Береза:
a–m = –1,302.10–9W5 + 4,958.10–7W4 – 5,502.10–5W3 +
+ 1,904.10–3W2 + 7,601W + 0,163 (5)
Дуб:
a–m = –1,096.10–9W5 + 4,547.10–7W4 – 5,222.10–5W3 +
+ 1,826.10–3W2 + 8,459.10–3W + 0,16 (5)
Общий характер зависимостей напоминает кривые, полученные W. Wissman и
H. Shauss [9, 10]. Кроме того, характер изменения влагопроводности древесины
соответствует уравнению проницаемости для массива древесины с непрерывно
меняющейся влажностью, предложенному Б.Д. Руденко
Что касается расчетной величины критерия фазового превращения (рис. 3),
то она также существенно зависит от влажности. Математическая обработка
результатов вычислений позволила получить следующие уравнения регрессии
для определения величины ?.
Сосна:
e = 4,18.10–9W4 + 1,127.10–6W3 – 3,62.10–4W2 +
+ 0,019W + 0,441 (8)
Лиственница:
e = 1,354.10–9W4 + 1,632.10–6W3 – 3,902.10–4W2 +
+ 0,02W + 0,439 (9)
Береза:
e = –1,411.10–8W4 + 4,99.10–6W3 – 5,975.10–4W2 +
+ 0,024W + 0,42 (10)
Дуб:
e = –2,027.10–8W4 + 6,387.10–6W3 – 6,855.10–4W2 +
+ 0,026W + 0,412 (11)
В дальнейшем, используя полученные выше соотношения для GП и i, а также
известное соотношение А.В. Лыкова [12] для плотности потока влаги
i = am n (un – up ), кг/(м2.с) , (12)
где am — коэффициент влагообмена, м/с;
n — плотность пара, кг/м3;
un — влажность испаряющей поверхности;
up — равновесная влажность среды,
было получено выражение для определения коэффициента влагообмена древесины
При этом выражение (13) справедливо для случая турбулентного обтекания сохнущего тела средой. Для случая ламинарного обтекания, которое, например, имеет место при естественной циркуляции агента, выражение (13) приобретает вид
где VЦ — скорость циркуляции, м/с;
VЦ.КР. — критическое значение скорости циркуляции при Re = 2320.
Выводы:
1. Коллоидная капиллярно-пористая структура древесины может быть промоделирована
системами микрокапилляров, представляющих собой части анатомических элементов
древесины и непостоянных микрокапилляров, радиус которых функционально
зависит от влажности древесины в гигроскопической области.
2. Для капиллярно-пористых тел, каким является древесина, влагообмен с
внешней средой происходит за счет удаления влаги из капилляров, выходящих
на поверхность.
Проблема капиллярного переноса достаточно хорошо изучена, однако к анализу
процессов влагоудаления при сушке подобный подход практически не применялся.
Для оценки вклада пленочного механизма в общий поток влаги может быть
использовано уравнение Дерягина-Нерпина.
3. Полученные в результате анализа моделей капиллярного испарения зависимости
нормированного коэффициента влагопроводности древесины показали их существенную
зависимость от влажности древесины.
Характер данных зависимостей напоминает данные известных немецких исследователей
свойств древесины W. Wissmann и H. Shauss, а также вполне соответствует
уравнению проницаемости для массива древесины, полученные Б.Д. Руденко.
4. В результате определения соотношения между капиллярным испарением и
пленочным переносом получены зависимости критерия фазового превращения
? в функции влажности древесины.
Значения ?, получаемые согласно указанным зависимостям, также вполне соответствуют
данным различных исследователей.
5. Значения коэффициента внешнего влагообмена древесины зависят от абсолютной
температуры, равновесной влажности среды и критерия фазового превращения,
а при ламинарном характере потока газа, обтекающего сохнущее тело, еще
и от скорости циркуляции.
Библиографический список
1. Перелыгин, Л.М. Строение древесины / Л.М. Перелыгин. М.: Гослесбумиздат,
1954 — 200 с.
2. Никитин, В.М. Химия древесины / В.М. Никитин, А.В. Аболенская, В.П.
Щеголев. М.: Лесн. пром-сть, 1978 — 368 с.
3. Химия древесины (т. II) / Перевод со второго американского издания
под ред. В.Д. Богомолова. М.-Л.: Гослесбумиздат, 1960.
4. Фенгел Д. Древесина (химия, ультраструктура, реакции) /Д. Фенгел, Г.
Вегенер. М.: Лесн. пром-сть, 1988.
5. Клеточная стенка древесины и ее изменения при химическом воздействии.
Рига: Зинатне, 1972 — 501 с.
6. Чудинов, Б.С. Вода в древесине / Б.С. Чудинов. Новосибирск: Наука,
1984 — 267 с.
7. Stamm, A.J. Laminar sorption and swelling theory for wood and cellulose
/ A.J. Stamm, W.E. Smith // Wood Sci. and Techn. 1969. V. 3, P. 301–323.
8. Чураев, Н.В. Физико-химия процессов массопереноса в пористых телах
/ Н.В. Чураев. М.: Химия, 1990 — 272 с.
9. Wissmann W. Ьber das verhalten von Baustoffen gegen Feuchtigkeitseinwirkungen
dus der ungebenden Luft: Diss T.H. / Wissmann W. Darmstadt. 1954. D. 17.
10. Shauss H. Phisikalische Vцrgange der Feuchtigkeits bewegung und ihre
Auswirkungen bei den vercheiedenen Verfahren der Holztrocknung / Diss
T.H. / Shauss H. Darmstadt. 1940. D. 87.
11. Сергеев, В.В. Повышение эффективности сушки пиломатериалов в камерах
малой мощности: дис. … д-ра техн. наук / Сергеев Валерий Васильевич. СПб.:
СПбЛТА им. С.М. Кирова, 1999.
12. Лыков, А.В. Теория тепло- и массопереноса / А.В. Лыков, Ю.А. Михайлов.
М.: Госэнергоиздат, 1963 — 535 с.
А.Г. Гороховский, Е.Е. Шишкина (УГЛТУ, г. Екатеринбург,
РФ).
По материалам доклада на III Международном евразийском симпозиуме «Деревообработка:
технологии, оборудование, менеджмент XXI века»
в рамках I Евро-Азиатского лесопромышленного форума,
30 сентября — 3 октября 2008 г., г. Екатеринбург, РФ



