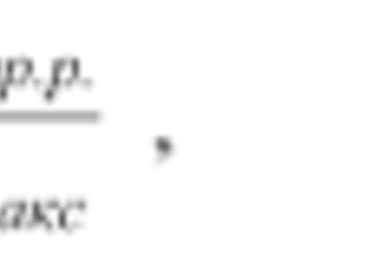Оптимизация раскроя пиловочника больших размеров с выпиливанием двух брусьев и двух пар боковых досок

На практике иногда рекомендуется осуществлять раскрой пиловочника больших размеров брусово-развальным способом с получением двух брусьев и двух пар боковых досок /3/. Такой постав называется четным. Важно знать оптимальные размеры брусьев и досок. Для решения задачи составляем математическую модель. В качестве критерия оптимальности выбираем объемный выход брусьев и боковых обрезных досок, получаемых при первом проходе брусово-развального способа раскроя. Целевую функцию можно представить в виде суммы площадей поперечных сечений двух брусьев и двух пар боковых обрезных досок

где: H — высота бруса,
A — ширина наружной пласти бруса,
T₁, T₂ — толщины первой и второй пары боковых досок,
в₁, в₂ — ширины первой и второй пар боковых досок.

Для составления уравнений связи воспользуемся теоремой Пифагора. Взаимосвязь диаметра бревна в вершинном торце с размерами брусьев и досок можно представить следующими уравнениями

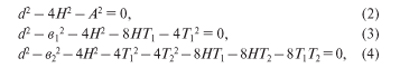
где: d — диаметр в верхнем торце бревна.

Полагаем, что математическая модель составлена. Для решения данной модели воспользуемся методом множителей Лагранжа. Функцию Лагранжа записываем в следующем виде:

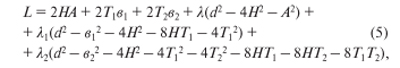
где: λ, λ₁, λ₂, — коэффициенты (множители) Лагранжа.

Находим частные производные от функции Лагранжа и приравниваем их нулю

Решаем данную систему уравнений (6) совместно с уравнениями связи.
Рассматриваем первое уравнение системы (6)

Рассматриваем последнее уравнение системы (6)

Пятое уравнение системы (6) можно представить в виде

В уравнение (9) подставляем равенство (8), получим

Рассматриваем четвертое уравнение системы (6)

Третье уравнение системы (6) можно записать в следующем виде:

В уравнение (12) подставляем равенство (11), получим

В последнее равенство (13) подставляем второе уравнение связи (3), получим

Тогда соотношение ширин досок можно определить по формуле

Из уравнения (13) можно определить ширину второй пары досок

Равенство (10) подставим в уравнение связи (4), получим

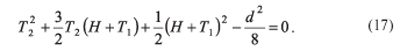
Решая полученное квадратное уравнение (17), получим

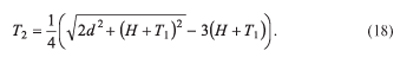
Рассматриваем второе уравнение системы (6), которое можно представить в виде:

Подставив в уравнение (19) равенство (7), получим

В равенство (20) подставим уравнение связи (2), получим

Возведем обе части равенства (21) в квадрат, получим

В последнее равенство (22) подставим уравнение связи (3) и освободимся от знаменателя

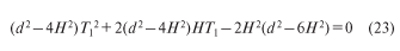
Решаем полученное квадратное уравнение (23), получим

Зная ширину пласти первой пары досок и используя уравнение связи (3), можно определить толщину этой пары досок по формуле

Зная ширины и толщины первой пары досок, можно, используя уравнение (16), определить ширины второй пары досок. Толщины второй пары досок можно определить, используя уравнение связи (4)

Таким образом, рассмотрена система уравнений (6) совместно с уравнениями связи и получены формулы для определения оптимальных размеров брусьев и досок. Однако в этих формулах размеры брусьев и досок взаимосвязаны. Поэтому определить оптимальные размеры брусьев и досок по данным формулам обычным методом не представляется возможным. Для решения данной задачи воспользуемся численным методом и определим размеры брусьев и досок по вышеприведенным формулам. Алгоритм решения задачи представляется ниже.
Для облегчения расчетов и анализа результатов полученные ранее формулы представляем в относительных единицах, полагая m_H = H/d .
Относительная ширина наружной пласти бруса

Относительная ширина первой пары досок

Относительная толщина первой пары досок

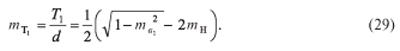
Относительная ширина второй пары досок

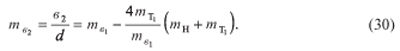
Относительная толщина второй пары досок

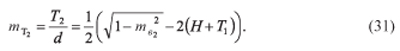
Относительная площадь поперечного сечения брусьев

Относительная площадь поперечного сечения досок

Суммарная площадь поперечных сечений брусьев и досок

Расчеты выполняются в два этапа. В начале задаемся толщиной бруса с градацией 0,01 d и определяем остальные размеры брусьев и досок, а также значение целевой функции. Далее определяем диапазон толщин брусьев, при которых целевая функция принимает наибольшее значение. Затем в этом оптимальном диапазоне изменяем толщину бруса с градацией 0,001 d и определяем все размеры брусьев и досок, а также величину целевой функции. 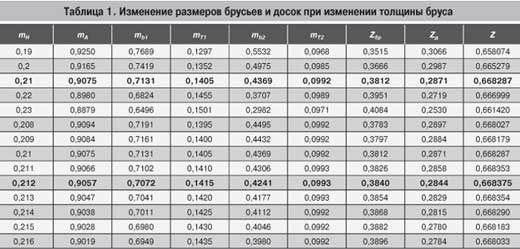По этим данным находим максимальное значение целевой функции и оптимальные размеры брусьев и досок. Результаты расчетов представлены в таблице 1.
Результаты расчетов показывают, что наибольший выход пилопродукции наблюдается при толщине бруса 0,212 d. Причем при увеличении толщины бруса их объем возрастает, а объем боковых досок уменьшается. Следовательно, предположение, сделанное ранее, подтверждается — имеется такое соотношение размеров брусьев и досок, при котором суммарный объем брусьев и досок становится наибольшим.
Важно знать оптимальные соотношения размеров брусьев и досок при оптимальной толщине бруса Н = 0,212 d, которые представлены в таблице 2.
Результаты таблицы 2 показывают, что λ = λ₂. Это значит, что отношение толщины бруса к ширине пласти его равно отношению толщины второй доски к ее ширине.
Тогда можно написать

В этом варианте раскроя пиловочника объем брусьев получается больше, чем объем досок. Пифагорическая зона в этом случае составляет 0,905 d. Анализируя данные таблицы 1, можно сделать вывод, что ширина наружной пласти второй пары досок в₂ должна быть равна двум толщинам бруса — 2Н. Подставляем это соотношение в уравнение (13), получим

Решаем это квадратное уравнение (36), получим

Подставляем полученное равенство (37) в уравнение связи (3), получим

Решая полученное квадратное уравнение (38), получим

Приравниваем равенство (39) и (22), получим

Возводим обе части равенства в квадрат и производим сложение подобных членов. В результате получаем биквадратное уравнение.

Решая это уравнение, получим одно значение корня, удовлетворяющее требованиям задачи, которое определяется по формуле

Таким образом, получено наиболее точное выражение для определения оптимальной толщины бруса.

Оптимальная толщина бруса для данного варианта раскроя составляет 0,212 от диаметра пиловочника.

Расчеты по формуле (42) показали, что оптимальное значение толщины бруса равно 0,2120176 от диаметра бревна. Для этого значения оптимальные размеры брусьев и досок будут следующими: ширина наружной пласти бруса А = 0,906 d; размеры первой пары досок — толщина Т₁ = 0,14155 d, ширина в₁ = 0,707 d; размеры второй пары досок — толщина Т₂ = 0,0993 d, ширина в₂ = 0,424 d.
Используя эти оптимальные соотношения, расчетные размеры брусьев и досок представлены в таблице 3.

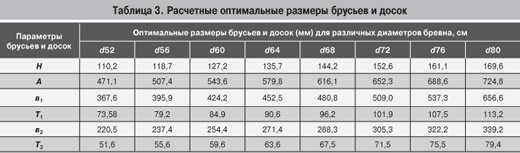
Результаты таблицы 3 показывают, что обрезные доски шириной 125÷150 мм целесообразно получать из брусьев, выпиливаемых из бревен диаметром 60÷72 см.
В этом случае боковые доски получаются толщиной 60÷100 мм. Учитывая эти оптимальные размеры брусьев и досок, можно составить оптимальные характеристики постава с получением максимально возможного выхода пилопродукции. Таким образом, задача решена — определены оптимальные размеры брусьев и досок, получаемых при распиловке пиловочника больших размеров брусово-развальным способом с выпиливанием двух брусьев и двух пар боковых досок.

Библиографический список

1. Пижурин А. А. Основы моделирования и оптимизации процессов деревообработки: Учебник для вузов/ Пижурин А. А., Розенблит М.С. — М.: Лесная пром-сть, 1988. — 293 с.
2. Аксенов П. П. Теоретические основы раскроя пиловочного сырья. — М.; Л.: Гослесбумиздат, 1960. — 216 с.
3. Ветшева В. Ф. Раскрой крупномерных бревен на пиломатериалы. — М.: Лесная пром-сть, 1976. — 168 с.
4. Агапов А. И. Определение оптимальных размеров основного постава брусо-развального способа раскроя бревен \ Сб. мат ВНТК «Наука-производство-технологии-экология» — Киров: ВятГУ, 2003. Том 5. ФАМ, ИСФ — с. 97–98.
5. Агапов А. И. Оптимизация раскроя крупномерных бревен \ Сб. мат ВНТК «Наука- производство-технологии-экология» — Киров: ВятГУ, 2003. Том 5. ФАМ, ИСФ — с. 99–100.
6. Агапов А. И. Определение оптимального соотношения высоты бруса и диаметра бревна при брусово-развальном способе раскроя бревен больших размеров \ Деп. рукопись в ВИНИТИ г. Москва, №499-В2004 26.03.04.
7. Агапов А. И. Теоретические предпосылки к расчету оптимальных размеров пилопродукции при раскрое пиловочника брусово-развальным способом \ Сб. мат. Международной НТК, Уральской гос.лесотехн.университет — г. Екатеринбург, 2007. 438 с. 116–119.
8. Агапов А. И. Определение оптимальной зоны размеров бруса и боковых досок при брусово-развальном способе раскроя пиловочника (статья) \ Сб. мат ВНТК «Наука-производство-технологии-экология» — Киров: ВятГУ, 2008. Том 4. ФАМ, ФСА 340 с (с. 139–140).
9. Агапов А. И. Оптимизация раскроя пиловочника больших размеров \ УДК 061.3:001 ББК Ч 215.16 ВНТК «Наука-производство-технология-экология» Сборник материалов. В 3т — Киров: Изд-во ГОУ ВПО Вят.ГУ, 2009, том 2. ХБ, БФ, ФАМ — с. 262 (с. 188–191).

---

Агапов А.И. (ВятГУ, г. Киров, РФ).
По материалам доклада на V Международном евразийском симпозиуме
«Деревообработка: технологии, оборудование, менеджмент XXI века»,
г. Екатеринбург, РФ, сентябрь 2010 г.