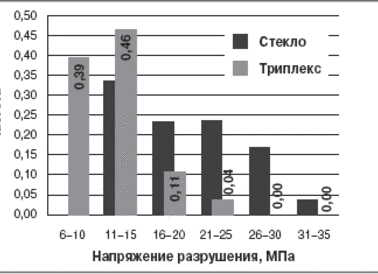
Расчеты силовых элементов из стекла

В современном мире стекло широко применяют не только для отделки фасадов или внутренних помещений здания, но также его используют в качестве основного материала опорных конструкций. Существуют специальные пакеты, моделирующие поведение конструкций из различных материалов различных форм под воздействием нагрузок. Основной целью данной работы является исследование поведения стеклянных ребер жесткости под воздействием внешних нагрузок.
В настоящее время для моделирования поведения различных конструкций все больше используется метод конечных элементов. Основными достоинствами этого метода являются гибкость и разнообразие сеток, стандартные приемы построения дискретных задач для произвольных областей, простота учета естественных краевых условий. Также данный метод позволяет получать более точные результаты не только за счет измельчения сетки, но и за счет увеличения порядка элементов, на которые разбивается область.
На основании метода конечных элементов создано множество математических пакетов. Целью данной работы является написание программы, легкой в использовании, основанной на методе конечных элементов, и моделирование поведения стеклянного ребра жесткости при помощи написанной программы.

Постановка задачи
Уравнение для прогиба бруса выглядит следующим образом:

• Share

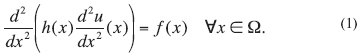
Здесь Q — область, в которой находится брус, h(x) — функция, представляющая собой произведение модуля упругости Юнга на момент инерции поперечного сечения, f(x) — функция внешней нагрузки.
В случае защемленного бруса граничные условия будут следующими (заданы отклонения и повороты краев бруса):

• Share

Вариационная формулировка задачи звучит следующим образом: требуется найти решение u(x) интегрального уравнения

• Share

где v(x) достаточно регулярная тестовая функция, от выбора которой решение u(x) не зависит, и обе функции u(x) и u(x) принадлежат некоторому пространству VЄH2(Q), функции которого удавлетворяют граничным условиям.

• Share

Примеры
Будем рассматривать стеклянные брусы с прямоугольным сечением. Рассмотрим случай закрепления бруса с торцов. Тогда граничные условия будут следующими

• Share

а пространство, в котором будем искать решение, примет вид

• Share

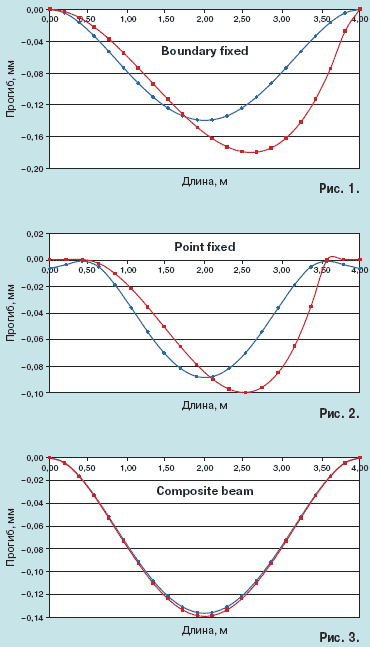
Для бруса размеров 4000 x 300 x 15 мм при силе в 440 Н величины прогибов при равномерной и точечной нагрузках привдены на рис. 1 (синим — при равномерной нагрузке, красным — при точечной).
Из графиков видно, что при точечной нагрузке брус прогибается сильнее, чем при равномерной, поэтому конструкции, в которых на брус приходится не точечаная нагрузка, а равномерная, являются более прочными.
При тройном закреплении стеклянных стенок расчеты можно производить не как для пластины, а как для бруса. В этом случае математическая модель выглядит следующим образом: уравнение (3) остается прежним, а граничные условия заменяются на следующие:

• Share

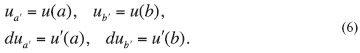
Здесь a` и b` не концы интервала, в котором находится брус, а координаты точек закрепления бруса.
На рис. 2 приведены графики прогиба бруса, закреп­ленного в двух внутренних точках, при равномерной и точечной нагрузке (синим — при равномерной нагрузке, красным — при точечной).
И опять же, при точечной нагрузке брус прогибается сильнее, чем при равномерной.
Теперь рассмотрим модель наборного бруса. Пусть есть один брус размера 4000 x 300 x 45 мм и 3 бруса размерами 4000 x 300 x 15 мм. Составим из последних трех один наборный брус размера 4000 x 300 x 45 мм. На рис.  3 изображены графики прогибов для такой модели (красным изображен прогиб наборного бруса, синим — прогиб цельного).
При одинаковой нагрузке прогиб наборного бруса для такой модели на 1,9% больше прогиба целого бруса, что позволяет использовать вместо литых широких брусьев наборные брусья, собранные из ряда более тонких сплоченных листов.

Основные результаты: